Geschwindigkeit-Zeit-Diagramme
In einem Geschwindigkeit-Zeit-Diagramm ist für die Bewegung eines Körpers der Zusammenhang zwischen seiner Geschwindigkeit v und der Zeit t dargestellt. Ein v-t-Diagramm für eine Bewegung mit konstantem Betrag der Geschwindigkeit (gleichförmige geradlinige Bewegung, gleichförmige Kreisbewegung) unterscheidet sich deutlich von einem v-t-Diagramm für eine Bewegung mit konstantem Betrag der Beschleunigung (gleichmäßig beschleunigte geradlinige Bewegung, freier Fall).
Im v-t-Diagramm hat der Anstieg des Graphen eine physikalische Bedeutung. Er ist gleich der Beschleunigung an der betreffenden Stelle.
Die Fläche unter dem Graphen ist gleich dem zurückgelegten Weg. Eine spezielle Art von v-t-Diagrammen sind Fahrtenschreiberdiagramme.
In einem Geschwindigkeit-Zeit-Diagramm ist für die Bewegung eines Körpers der Zusammenhang zwischen seiner Geschwindigkeit v und der Zeit t dargestellt. Man bezeichnet solche Diagramme auch als v-t-Diagramme, Zeit-Geschwindigkeit-Diagramme oder t-v-Diagramme. Für jede Art von Bewegung ergibt sich ein charakteristisches v-t-Diagramm.
Bewegungen mit konstantem Betrag der Geschwindigkeit
Solche Bewegungen mit einem konstanten Betrag der Geschwindigkeit sind die gleichförmige geradlinige Bewegung und die gleichförmige Kreisbewegung. Bei ihnen bleibt die Geschwindigkeit immer gleich. Es gilt:
| v = konstant |
Als Graph ergibt sich eine Gerade parallel zur t-Achse (Bild 1).
-
v-t-Diagramm für Bewegungen mit konstantem Betrag der Geschwindigkeit
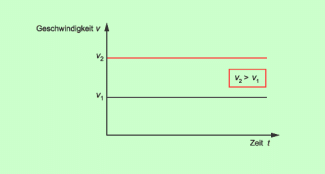
Je größer die Geschwindigkeit ist, umso höher liegt der Graph.
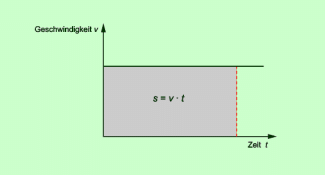
Die Fläche unter dem Graphen ist gleich dem zurückgelegten Weg (Bild 2).
-
Im v-t-Diagramm ist die Fläche unter dem Graphen gleich dem Weg
Bewegungen mit konstantem Betrag der Beschleunigung längs der Bahn
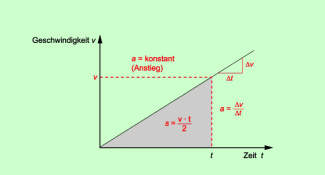
Solche Bewegungen, bei denen die Beschleunigung längs der Bahn einen konstanten Betrag hat, sind die gleichmäßig beschleunigte geradlinige Bewegung, die gleichmäßig beschleunigte Kreisbewegung und der freie Fall als eine spezielle gleichmäßig beschleunigte geradlinige Bewegung. Bei diesen Bewegungen ergibt sich als Graph eine ansteigende Gerade. Je größer die Beschleunigung ist, desto steiler verläuft der Graph (Bild 3).
-
v-t-Diagramm für Bewegungen mit konstantem Betrag der Beschleunigung
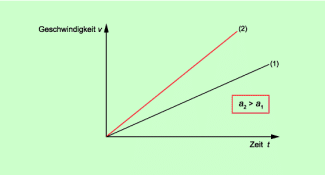
Der Anstieg des Graphen ist im v-t-Diagramm gleich der Beschleunigung. Die Fläche unter dem Graphen ist gleich dem zurückgelegten Weg (Bild 4)
Bei ungleichmäßig beschleunigten Bewegungen hängt die Form des Graphen vom Verlauf der Bewegung ab, ist aber keine Gerade.
-
Im v-t-Diagramm haben der Anstieg des Graphen und die Fläche unter dem Graphen eines physikalische Bedeutung
Fahrtenschreiberdiagramme
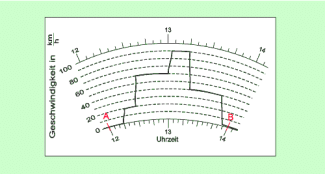
Eine besondere Form von v-t-Diagrammen sind Fahrtenschreiberdiagramme. Solche Diagramme erhält man durch Fahrtenschreiber, die für LKW und Busse vorgeschrieben sind. Mit einem solchen Fahrtenschreiber wird auf einer kreisförmigen Scheibe die jeweilige Geschwindigkeit aufgezeichnet.
-
Fahrtenschreiberdiagramm eines Busses

L. Meyer, Potsdam
Bild 6 zeigt eine vereinfachte Darstellung eines Fahrtenschreiberdiagramms. Aus einem solchen Diagramm ist ablesbar:
- die Geschwindigkeit zu jedem beliebigen Zeitpunkt,
- die Länge von Fahrpausen.
Gerade das Letzte ist wichtig, weil aus Gründen der Verkehrssicherheit für Bus- und LKW-Fahrer Pausenzeiten gesetzlich vorgeschrieben sind. Auch PKW-Fahrer sollten bei längeren Fahrten Pausen einplanen.
-
Fahrtenschreiberdiagramm (vereinfacht)