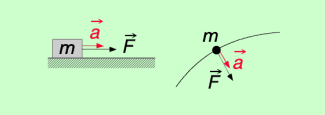Newtonsches Grundgesetz
Zwischen Kraft, Masse und Beschleunigung gilt folgender Zusammenhang:
| F | auf den Körper einwirkende Kraft | ||
| m | Masse des Körpers | ||
| a | Beschleunigung des Körpers |
Dieses Gesetz wurde von ISAAC NEWTON (1643-1727) entdeckt und beinhaltet einen grundlegenden Zusammenhang zwischen Kraft und Bewegung.
Zwischen Kraft, Masse und Beschleunigung gilt folgender Zusammenhang:
| F | auf den Körper einwirkende Kraft | ||
| m | Masse des Körpers | ||
| a | Beschleunigung des Körpers |
Dieses Gesetz wurde von dem berühmten englischen Naturforscher ISAAC NEWTON (1643-1727) entdeckt und beinhaltet einen grundlegenden Zusammenhang zwischen Kraft und Bewegung. Es wird auch als 2. newtonsches Gesetz, als 2. newtonsches Axiom oder als Grundgesetz der Mechanik bezeichnet. Insbesondere die letzte Bezeichnung spiegelt die Bedeutung dieses Gesetzes wider.
Aus dem Gesetz ergibt sich:
Die Beschleunigung eines Körpers ist umso größer,
- je größer die auf den Körper wirkende Kraft ist und
- je kleiner die Masse des Körpers ist.
Dabei ist zu beachten: Sowohl die Kraft als auch die Beschleunigung sind gerichtete (vektorielle) Größen. Die Beschleunigung des Körpers erfolgt immer in die Richtung, in die die Kraft wirkt (Bild 1).
Dieses Gesetz bewirkt z.B., dass eine Schwimmerin mit einer größeren Absprungkraft eine größere Beschleunigung erreicht als eine gleich schwere Schwimmerin mit kleinerer Absprungkraft. Dagegen braucht eine Schwimmerin mit einer größeren Masse eine größere Kraft, um die gleiche Beschleunigung zu erreichen wie eine Schwimmerin mit kleinerer Masse.
Aus dem newtonschen Grundgesetz ergibt sich auch die Einheit für die Kraft, das Newton. Setzt man in die Gleichung die Größen mit dem Zahlenwert 1 ein, so erhält man: