Approximation einer Binomialverteilung
Bei der praktischen Anwendung der Binomialverteilung treten nicht selten große oder sogar sehr große Werte von n (etwa ) auf, wodurch das Berechnen der Wahrscheinlichkeiten aufgrund der dabei zu ermittelnden Fakultäten und Potenzen sehr zeitaufwendig wird. Schon frühzeitig versuchte man deshalb, Näherungsformeln für die Binomialverteilung zu finden.
Hier ist es (unter bestimmten Voraussetzungen) günstig, die Binomialverteilung durch eine POISSON-Verteilung oder eine Normalverteilung zu approximieren und entsprechende Näherungsformeln anzuwenden.
Approximation durch eine POISSON-Verteilung
Der französische Mathematiker und Physiker SIMÉON DENIS POISSON (1781 bis 1840) untersuchte das Verhalten von speziell für wachsendes n, wobei er aber das Parameterprodukt , d.h. den Erwartungswert EX der -verteilten Zufallsgröße X, konstant hielt.
Beispiel: Es sollen (gewissermaßen auf den Spuren von POISSON) einzelne Wahrscheinlichkeiten
für größer werdendes n mit berechnet werden.
Für , und ergibt sich die folgende Tabelle.
![]()
Die gewonnenen Resultate legen die Vermutung nahe, dass sich die Wahrscheinlichkeiten der Binomialverteilung für wachsendes n und konstantes einem endlichen und von null verschiedenen Grenzwert nähern.
Diese Erfahrung führte zu dem folgenden Grenzwertsatz von POISSON:
- Grenzwertsatz von POISSON: Es gilt:
(wobei e = 2,718281... die eulersche Zahl ist)
Das bedeutet: Bei kleiner Erfolgswahrscheinlichkeit p kann die Binomialverteilung durch die (später nach POISSON benannte) POISSON-Verteilung approximiert werden.
Die Anwendung der poissonschen Näherung für die Binomialverteilung ist sinnvoll für (als Faustregel), d.h. für gilt:
Durch den Vergleich von zwei verschiedenartigen Fällen von Näherungen der Binomialverteilung durch die POISSON-Verteilung kann man (interaktiv) verdeutlichen, dass die Anwendung der Faustregel sinnvoll ist. Vergleiche das Histogramm von (in der folgenden Abbildung links) und das Punktdiagramm von (in der folgenden Abbildung rechts).
-
Approximation der Binomialverteilung durch eine POISSON-Verteilung (links: Faustregel nicht erfüllt; rechts: Faustregel erfüllt)
Die Approximation der Binomialverteilung durch eine POISSON-Verteilung gestattet es, die Wahrscheinlichkeiten der Binomialverteilung relativ bequem zu berechnen (dies allerdings nur für kleine p).
Approximation durch eine Normalverteilung
Eine weitere Approximation der Binomialverteilung , und zwar durch eine Normalverteilung , ermöglicht der Grenzwertsatz von MOIVRE-LAPLACE. Er führt zu den folgenden Näherungsformeln:
- Für (als Faustregel) gilt:
(mit als Funktion der gaußschen Glockenkurve und Dichtefunktion der )
(mit als Stammfunktion von , wobei und gewählt wurden)
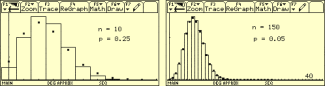
Durch den Vergleich von zwei verschiedenartigen Fällen von Näherungen der Binomialverteilung durch die Normalverteilung kann man (interaktiv) verdeutlichen, dass die Anwendung der Faustregel sinnvoll ist. Vergleiche das Histogramm von (in der folgenden Abbildung links) und den Graph der Dichtefunktion (in der folgenden Abbildung rechts).
-
Approximation der Binomialverteilung durch eine Normalverteilung (links: Faustregel nicht erfüllt; rechts: Faustregel erfüllt)

Im Gegensatz zur Approximation der Binomialverteilung durch die POISSON-Verteilung, die nur für kleine Wahrscheinlichkeiten p eine gute Näherung liefert, kann man die Approximation durch die Normalverteilung für jedes p mit anwenden, wenn n nur hinreichend groß ist.
Wir betrachten dazu ein Beispiel.
Beispiel: Für welche Wahrscheinlichkeiten p benötigt man die wenigsten n, damit die für die Approximation der Binomialverteilung durch die Normalverteilung geltende Faustregel erfüllt ist?
Lösung:
Die Aufgabe könnte durch „wildes“ Probieren bearbeitet werden. Eine analytische Lösung ist jedoch z.B. dadurch möglich, dass die Faustregel umgeformt wird zu . Die wenigsten n werden dann benötigt, wenn der Funktionswert maximal wird. Der Graph (eine quadratische Parabel) von f hat an der Stelle 0,5 einen Hochpunkt.
Die herausgehobene Stellung des Wertes wird auch dadurch bestätigt, dass für der maximal mögliche Fehler, der bei der Approximation der Binomialverteilung durch die Normalverteilung begangen wird, am kleinsten ist. In dem Maße, wie sich p von 0,5 entfernt, wird die Fehlerschranke immer größer.
Das Histogramm links in der vorangegangenen Abbildung legt die Vermutung nahe, dass man durchaus noch „brauchbare“ Näherungen der Binomialverteilung durch die Normalverteilung erhalten kann, wenn man die angegebene Faustregel abschwächst.
Dies ist in der Tat der Fall. Wenn nur „grobe“ Näherungen erforderlich sind, verwendet man auch die folgende Faustregel:

