Kenngrößen von Zufallsgrößen
Eine Zufallsgröße wird vollständig durch ihre Verteilungsfunktion beschrieben. Diese gibt an, welche Werte die Zufallsgröße annehmen kann und mit welchen Wahrscheinlichkeiten sie dies tut.
In der Praxis möchte man allerdings meist mit möglichst wenigen, aber typischen Angaben auskommen, denn oftmals reicht schon eine grobe Vorstellung von der Zufallsgröße aus. Es kommt hinzu, dass die Verteilungsfunktion mitunter gar nicht oder nur schwer bestimmbar ist.
Man sucht deshalb nach Kenngrößen (manchmal spricht man auch von Parametern), die einen hinreichenden Aufschluss und eine quantitative Charakterisierung einer Zufallsgröße ermöglichen. Dies leisten Kenngrößen wie Erwartungswert, Median und Modalwert sowie die Streuung (bzw. Varianz) der Zufallsgröße.
Zur Charakterisierung der Asymmetrie einer Zufallsgröße benutzt man darüber hinaus die Kenngröße Schiefe. Eine Definition dieser Kenngröße geht auf den Vater der mathematischen Statistik KARL PEARSON (1857 bis 1936) zurück.
-
Karl Pearson (1857 bis 1936)

Erwartungswert einer Zufallsgröße
Die wichtigste und einfachste derartige Angabe ist der Erwartungswert einer Zufallsgröße X (Abkürzung EX oder ).
- Der Erwartungswert einer diskreten Zufallsgröße X, die die Werte mit den dazugehörigen Wahrscheinlichkeiten annehmen kann, ist wie folgt definiert:
Für eine stetige Zufallsgröße X mit der Dichte(funktion) f gilt:
Die herausgehobene Stellung des Erwartungswertes hängt vor allem mit folgenden Umständen zusammen:
- Bei n unabhängigen Realisierungen einer Zufallsgröße X stabilisiert sich das arithmetische Mittel der Ergebnisse für große n beim Erwartungswert der Zufallsgröße, d.h. das empirisch gewonnene arithmetische Mittel kann als Schätzwert für den Erwartungswert dienen. Andererseits ermöglicht der Erwartungswert eine Prognose über das arithmetische Mittel bei vielen Beobachtungswerten einer Zufallsgröße X.
- Bei einer Reihe von Zufallsgrößen, deren Verteilungen nur von einem Parameter abhängen, reicht (wie etwa bei der POISSON-Verteilung) die Kenntnis des Erwartungswertes für die vollständige Charakterisierung der Zufallsgröße aus.
Bei praktischen Problemen kann man mitunter aufgrund von inhaltlichen Überlegungen vom Vorliegen einer POISSON-Verteilung ausgehen. Dann beschreibt das arithmetische Mittel der Beobachtungswerte die Zufallsgröße hinreichend. - Bei symmetrischen Verteilungen (wie etwa der Normalverteilung) bildet der Erwartungswert eine Art Zentrum dieser Verteilung, um das sich alle anderen Werte mehr oder weniger eng gruppieren.
Der Erwartungswert ist in diesen Fällen ein typischer Wert der Zufallsgröße. So repräsentiert z.B. bei einem n-mal unabhängig durchgeführten Messvorgang, von dem man annehmen kann, dass er einer normalverteilten Zufallsgröße entspricht, der Erwartungswert den tatsächlich zu messenden Wert.
Hat man es allerdings mit einer asymmetrischen, schiefen Verteilung zu tun, so beschreibt die Lage des Erwartungswertes im Allgemeinen keinen typischen Wert.
- Beispiel: Die Lebensdauer von Glühlampen kann durch die in der folgenden Abbildung wiedergegebene Dichtefunktion beschrieben werden.
-
Beispiel einer asymmetrischen, schiefen Verteilung

Der Erwartungswert ist kein typischer Wert, d.h. in einem solchen Fall wird man versuchen, die Verteilung durch weitere Kenngrößen zu beschreiben. Das ist auch deshalb erforderlich, weil nicht jede Zufallsgröße einen Erwartungswert besitzt.
Median und Modalwert einer Zufallsgröße
Weitere Kenngrößen einer Zufallsgröße sind der Median und der Modalwert.
- Median der Zufallsgröße X mit der Verteilungsfunktion F heißt der Argumentwert , für den die Ungleichungen gelten.
Wenn die Funktion F stetig ist, so gibt es mindestens eine Zahl mit . Der Median halbiert die Verteilung. Man spricht auch vom mittelsten Wert der Verteilung.
- Als Modalwert M einer Zufallsgröße bezeichnet man einen solchen Wert, für den die Einzelwahrscheinlichkeit (diskrete Zufallsgröße) bzw. die Wahrscheinlichkeitsdichte (stetige Zufallsgröße) maximal wird.
Man spricht auch vom häufigsten Wert.
-
Beispiel für das Nichtzusammenfallen von Median und Erwartungswert einer Zufallsgröße
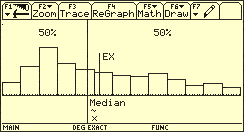
-
Beispiel für das Nichtzusammenfallen von Modalwert und Erwartungswert einer Zufallsgröße
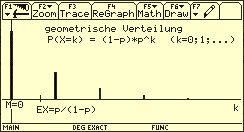
Streuung (bzw. Varianz) einer Zufallsgröße
Zufallsgrößen mit gleichem Erwartungswert unterscheiden sich ggf. noch wesentlich voneinander, denn die einzelnen Werte der Zufallsgrößen können in unterschiedlicher Weise um den Erwartungswert streuen.
-
Zufallsgrößen mit gleichem Erwartungswert, aber unterschiedlicher Streuung
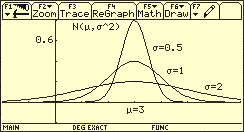
Das gebräuchlichste Maß der Streuung (bzw. Varianz) ist heute die mittlere quadratische Abweichung.
- Die Streuung (bzw. Varianz) einer diskreten Zufallsgröße X ist folgendermaßen definiert:
Die Streuung (bzw. Varianz) einer stetigen Zufallsgröße X mit der Dichte f ist definiert durch:
Aufgrund der Linearität des Erwartungswertes erhält man durch einfache algebraische Umformung die folgende (für Berechnungen nützliche) Formel:
Bezüglich der Streuung von Zufallsgrößen lässt sich Folgendes feststellen:
- Die Streuung ist ein quantitatives Maß für den Grad der Verstreutheit einer Zufallsgröße X. Bei kleiner Streuung sind große Abweichungen der Zufallsgröße X vom Erwartungswert EX eher unwahrscheinlich. Umgekehrt liegen bei einer großen Streuung nicht alle Werte von X in der Nähe des Erwartungswertes.
- Eine Zufallsgröße besitzt genau dann die Streuung 0, wenn diese Zufallsgröße mit Wahrscheinlichkeit 1 nur einen einzigen Wert annimmt. Dieser ist dann gleichzeitig der Erwartungswert.
Man spricht in diesem Fall von einer Einpunktverteilung. Dies deckt sich auch mit den inhaltlichen Vorstellungen, die man von der Streuung besitzt. - Die Streuung ist von der speziellen Wahl des Koordinatenursprungs unabhängig. Sie kennzeichnet die Ausbreitung einer Verteilung. Deshalb bezeichnet man sie bisweilen auch als einen Ausbreitungsparameter der Zufallsgröße.
Nicht wenige Zufallsgrößen besitzen eine asymmetrische Verteilung. Zur Charakterisierung der Asymmetrie benutzt man die Kenngröße Schiefe. Für diese Kenngröße gibt es unterschiedliche Definitionen. Wir geben hier die relativ einfache, auf den Vater der mathematischen Statistik KARL PEARSON (1857 bis 1936) zurückgehende Fassung an.
- Gemäß der Definition durch KARL PEARSON ist die Schiefe der Quotient aus der Differenz des Erwartungswertes EX und des Modalwertes M sowie der Standardabweichung DX von X, d.h. für die Schiefe gilt:
Die Normalverteilung als eine symmetrische Verteilung besitzt die Schiefe 0. Die Exponentialverteilung, bei der der „längere Teil“ rechts vom Erwartungswert liegt, besitzt eine positive Schiefe, und zwar mit dem Wert 1, da und ist.
-
Exponentialverteilung
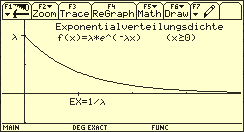
Suche nach passenden Schlagwörtern
- Median
- arithmetisches Mittel
- Exponentialverteilung
- Poisson-Verteilung
- Standardabweichung
- Varianz
- Verteilungen
- Normalverteilung
- Wahrscheinlichkeiten
- schiefe Verteilung
- Schiefe
- Erwartungswert
- Verteilungsfunktion
- Modalwert
- mittlere quadratische Abweichung
- stetige Zufallsgröße
- Zufallsgrößen
- Pearson
- Streuung
- diskrete Zufallsgröße

