Eigenschaften und Anwendungen des Skalarprodukts von Vektoren

Das Skalarprodukt zweier Vektoren der Ebene oder des Raumes ermöglicht es, die Orthogonalitätsbedingung für zwei Vektoren sehr einfach zu formulieren. Dazu werden zunächst die Eigenschaften des Skalarproduktes näher betrachtet.

Eigenschaften des Skalarprodukts

Für beliebige Vektoren $\vec{a}, \vec{b} u n d \vec{c}$ sowie für jede reelle Zahl t gilt:

a → ⋅ b → = b → ⋅ a → (Kommutativität)
$\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$ (Distributivität)
$(t \vec{a}) \cdot \vec{b} = t (\vec{a} \cdot \vec{b})$
${\vec{a}}^{2} \geq 0, w o b e i {\vec{a}}^{2} = 0 g e n a u d a n n, w e n n \vec{a} = \vec{o}$

Für das Skalarprodukt zweier Vektoren der Ebene oder des Raumes, die durch ihre Koordinaten gegeben sind, gilt:
$\vec{a} \cdot \vec{b} = a_{x} b_{x} + a_{y} b_{y} b z w . \vec{a} \cdot \vec{b} = a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z}$

Dies ermöglicht es, die Orthogonalitätsbedingung für zwei Vektoren sehr einfach zu formulieren. Es gilt der folgende Satz:

Sind bezüglich eines Koordinatensystems die beiden Vektoren
$\vec{a} = (\begin{matrix} a_{x} \\ a_{y} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{x} \\ b_{y} \end{matrix})$
in der Ebene gegeben, dann gilt $\vec{a} ⊥ \vec{b}$ genau dann, wenn $a_{x} b_{x} + a_{y} b_{y} = 0$ .
Sind bezüglich eines Koordinatensystems die beiden Vektoren
$\vec{a} = (\begin{matrix} a_{x} \\ a_{y} \\ a_{z} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{x} \\ b_{y} \\ b_{z} \end{matrix})$
im Raum gegeben, dann gilt $\vec{a} ⊥ \vec{b}$ genau dann, wenn $a_{x} b_{x} + a_{y} b_{y} + a_{z} b_{z} = 0$ .

Bezeichnet man mit ${\vec{e}}_{1}, {\vec{e}}_{2} b z w . {\vec{e}}_{3}$ die Einheitsvektoren in Richtung der Achsen eines kartesischen Koordinatensystems, so folgt speziell:
${\vec{e}}_{1} \cdot {\vec{e}}_{2} = {\vec{e}}_{1} \cdot {\vec{e}}_{3} = {\vec{e}}_{2} \cdot {\vec{e}}_{3} = 0$

Beispiel 1: Es ist zu überprüfen, welcher der drei Vektoren
$\vec{a} = (\begin{matrix} 3 \\ 5 \\ - 1 \end{matrix}), \vec{b} = (\begin{matrix} - 1 \\ 4 \\ 2 \end{matrix}) u n d \vec{c} = (\begin{matrix} - 2 \\ 1,8 \\ 3 \end{matrix})$
zu einem der anderen beiden orthogonal ist.

Es gilt: $\vec{a} \cdot \vec{b} = 15, \vec{a} \cdot \vec{c} = 0 u n d \vec{b} \cdot \vec{c} = 15,2$
Also sind lediglich die Vektoren $\vec{a} u n d \vec{c}$ zueinander senkrecht.

Beispiel 2: Gegeben seien in der Ebene die beiden Geraden
$g_{1} : \vec{x} = (\begin{matrix} 1 \\ 2 \end{matrix}) + t (\begin{matrix} 2 \\ 2 \end{matrix}), t \in R, u n d g_{2} : y = - x + 3$ ,
die einander im Punkt S(1; 2) schneiden.

Untersuchung von Geraden auf Orthogonalität

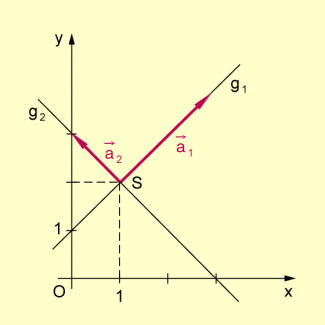
Aus der Abbildung ist zu entnehmen, dass diese beiden Geraden zueinander senkrecht sein könnten. Dies soll nun rechnerisch nachgeprüft werden.
Dazu wird von $g_{1} u n d g_{2}$ jeweils einen Richtungsvektor bestimmt:
Aus der Gleichung von $g_{1}$ kann man sofort einen Richtungsvektor dieser Geraden ablesen, nämlich
${\vec{a}}_{1} = (\begin{matrix} 2 \\ 2 \end{matrix})$ .

Da der Anstieg der Geraden $g_{2}$ den Wert -1 hat, lässt sich aus dem Anstiegsdreieck
${\vec{a}}_{2} = (\begin{matrix} - 1 \\ 1 \end{matrix})$
als ein Richtungsvektor von $g_{2}$ bestimmen.

Bildet man nun das Skalarprodukt dieser beiden Richtungsvektoren, so ergibt sich
${\vec{a}}_{1} \cdot {\vec{a}}_{2} = (\begin{matrix} 2 \\ 2 \end{matrix}) \cdot (\begin{matrix} - 1 \\ 1 \end{matrix}) = - 2 + 2 = 0$ .

Die Vektoren ${\vec{a}}_{1} u n d {\vec{a}}_{2}$ sind also zueinander senkrecht. Da aber ${\vec{a}}_{1} u n d {\vec{a}}_{2}$ die Richtungen von $g_{1} u n d g_{2}$ beschreiben, sind folglich auch $g_{1} u n d g_{2}$ zueinander senkrecht und die Vermutung aus der Abbildung wurde bestätigt.

Das Skalarprodukt von Vektoren findet weiterhin Anwendung u.a.

bei der Berechnung von Schnittwinkeln;
bei der Ermittlung von Abständen zwischen Punkten, Geraden und Ebenen;
beim Arbeiten mit Matrizen;
als Hilfsmittel beim Aufstellen von Tangenten- oder Tangentialebenengleichungen

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Eigenschaften und Anwendungen des Skalarprodukts von Vektoren

Eigenschaften des Skalarprodukts

Rechtliches

Einloggen