Geometrische Verteilung
Die geometrische Verteilung ist ein Spezialfall der PASCALschen Verteilung, die ihren Namen zu Ehren BLAISE PASCALS (1623 bis 1662) erhielt.
Beispiel: Von Würfelbrettspielen, wie etwa dem Mensch-ärgere-dich-nicht-Spiel, ist die Situation bekannt, dass man nach wiederholten Versuchen immer noch auf die erste Sechs wartet.
Dieses Warten auf das erstmalige Eintreten eines bestimmten Ereignisses, d.h. das „Warten auf den ersten Erfolg“, lässt sich mathematisch recht gut beschreiben durch die zufällige Anzahl X von Durchführungen eines BERNOULLI-Experiments mit der Erfolgswahrscheinlichkeit p bis zum Eintreten des ersten Erfolgs (wobei bis zum Eintreten des „ersten Erfolges“ unendlich viele Durchführungen benötigt werden können).
Aus dem zugehörigen Baumdiagramm kann man die Wahrscheinlichkeitsverteilung der Zufallsgröße X ablesen.
-
Baumdiagramm einer geometrischen Verteilung
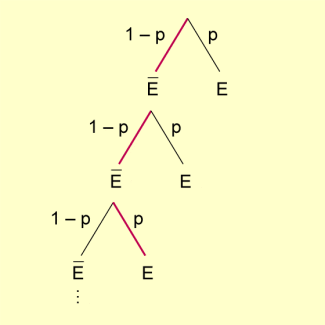
Es gilt:
Dies führt zu der folgenden Definition:
- Definition: Eine diskrete Zufallsgröße X heißt geometrisch verteilt mit dem (Erfolgs-)Parameter p , wenn sie ihre Werte k mit der Wahrscheinlichkeit annimmt.
Der Name „geometrisch verteilt“ ist gewählt worden, weil die Wahrscheinlichkeiten Glieder einer geometrischen Zahlenfolge sind, und zwar mit dem konstanten Quotienten
und der rekursiven Bildungsvorschrift .
Anmerkung: Die Bezeichnungen „geometrische Verteilung“ und „geometrische Wahrscheinlichkeit“ klingen zwar ähnlich, werden aber für verschiedenartige Zufallsexperimente verwandt. In dieser Hinsicht ist also Vorsicht geboten.
Unter Verwendung eines CAS kann man sich schnell eine Vorstellung vom Graphen der Wahrscheinlichkeitsfunktion der geometrischen Verteilung verschaffen. Dabei gelangt man zu der Vermutung, dass diese Verteilung gut durch die Funktion f mit zu approxieren sein müsste.
-
Wahrscheinlichkeitsfunktion einer geometrischen Verteilung
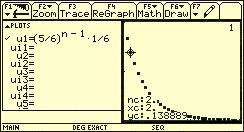
In der Tat ist die geometrische Verteilung das diskrete Analogon zur Exponentialverteilung.
Die geometrische Verteilung ist also die Verteilung der zufälligen Anzahl der Misserfolge vor dem ersten Erfolg bei einer BERNOULLI-Kette. Dauert die Realisierung des zu einer geometrisch verteilten Zufallsgröße X gehörenden BERNOULLI-Experiments genau eine Zeiteinheit, so gibt X die Wartezeit bis zum ersten Erfolg an. Man spricht in diesem Zusammenhang in der Stochastik auch von Wartezeitproblemen. Wir betrachten dazu ein Beispiel:
Beispiel: Beim Mensch-ärgere-dich-nicht-Spiel hat die Sechs eine besondere Bedeutung. Erst dann, wenn man eine Sechs gewürfelt hat, darf man mit dem Spiel beginnen. Erst nach einer gewürfelten Sechs kann ein weiterer Stein eingesetzt und nach einer Sechs darf zusätzlich einmal gewürfelt werden.
Mit welcher Wahrscheinlichkeit wird man, nachdem man einen Stein schon einsetzen durfte, d.h. mit dem Spiel starten durfte, erst beim vierten Würfeln (Fall 1), frühestens beim vierten Würfeln (Fall 2) erneut eine Sechs erreichen?
Mit welcher Wahrscheinlichkeit kann man erst in der dritten Runde (Fall 3), spätestens in der dritten Runde (Fall 4) durch Einsetzen eines Steines am Spiel teilnehmen, wenn man in jeder Runde zum Erreichen einer Sechs maximal dreimal würfeln darf?
Lösung:
Es sei X die zufällige Anzahl der Würfe des Mitspielers bis zu einer Sechs mit .
Dann erhält man:
![]()
Die im Beispiel aufgetretene Wahrscheinlichkeit, frühestens im i-ten Versuch den ersten Erfolg zu haben, kann auch auf eine einfachere und direktere Weise berechnet werden.
Dazu muss man folgende Umformung vornehmen:
(wobei für die Berechnung der Summe die Summenformel für geometrische Reihen angewendet wurde)
Moderne Taschencomputer ermöglichen es, die unendliche Reihe unmittelbar zu berechnen.
Es gilt also die folgende Formel:
Analog oder über das Gegenereignis erhält man:
Bei der Bearbeitung des obigen Beispiels liegt die Frage nahe, wie lange man im Mittel würfeln muss, um erstmals eine Sechs zu erhalten, d.h. man fragt nach dem Erwartungswert einer geometrisch verteilten Zufallsgröße.
Es gilt folgender Satz:
- Satz: Eine mit dem Parameter p geometrisch verteilte Zufallsgröße X besitzt als Kenngrößen den Erwartungswert und die Streuung (bzw. Varianz) .
Beweis (für den Erwartungswert):

