Nullstellen ganzrationaler Funktionen (dritten und höheren Grades)

Näherungsweise kann man Nullstellen auch grafisch bestimmen. Man zeichnet den Graphen der Funktion und liest den Abszissenwert beim Schnittpunkt des Graphen mit der x-Achse als Nullstelle ab.

Bei ganzrationalen Funktionen vom Grad $\text{n}\ge \text{3}$ ergeben sich bei der Nullstellenbestimmung Gleichungen, für die man (anders als bei linearen und quadratischen Funktionen) im Allgemeinen keine Lösungsformeln mehr zur Verfügung hat. Für Gleichungen dritten und vierten Grades wurden zwar bereits im 16. Jahrhundert „Lösungsformeln“ entwickelt, die jedoch in der Ausführung so kompliziert sind, dass sie praktisch kaum verwendet werden. Für eine Reihe von Problemen lassen sich die Nullstellen mit Näherungsverfahren oder mit einem Computeralgebrasystem bestimmen.

Sonderfälle

Für einige Sonderfälle existieren auch spezielle Lösungsverfahren, z.B. Lösen durch Ausklammern.

• Beispiel 1: Die Nullstellen der Funktion $f\left(x\right)=x^3-2x^2-3x$ sollen ermittelt werden.

Nullsetzen von f(x) ergibt:
$x^3-2x^2-3x=0$
Auf der linken Seite kann man x ausklammern:
$x\left(x^2-2x-3\right)=0$
Ist ein Produkt gleich null, so ist mindestens einer der Faktoren gleich null, d.h., es ist:
$x_1=0$ oder $x^2-2x-3=0$
Die Lösung der quadratischen Gleichung ergibt:
$x_2=3$ und $x_3=-1$

Ein anderes spezielles Lösungsverfahren ist das Lösen durch Substitution, wenn man es mit so genannten biquadratischen Gleichungen zu tun hat.

• Beispiel 2: Gegeben sei die Funktion $f\left(x\right)=x^4-19x^2+48$, man ermittle die Nullstellen.

Die Gleichung $x^4-19x^2+48=0$ ist zu lösen. Man setzt $z=x^2$.
Mit dieser Substitution erhält man eine quadratische Gleichung in z:
$z^2-19z+48=0$
Diese hat die Lösungen $z_1=3$ und $z_2=16$.
Nun wird die Substitution rückgängig gemacht, und die Gleichungen $x^2=3$ und $x^2=16$ werden gelöst. Das führt zu folgenden Nullstellen:
$x_1=\sqrt{3};x_2=-\sqrt{3};x_3=4;x_4=-4$

Ein weiteres Lösungsverfahren ist das Lösen durch schrittweises Faktorisieren einer ganzrationalen Funktion mithilfe ihrer Nullstellen. Grundlage dafür ist der folgende Zusammenhang:

• Wenn $x_0$ eine Nullstelle der ganzrationalen Funktion f vom Grad n (mit $n\in \mathbb{N}$), d.h. mit der Form $f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\mathrm{...}+a_{1}x+a_0$ ist, dann gibt es eine Zerlegung der Form $f(x)=(x-x_0)\cdot g(x)$. Dabei ist g(x) eine Funktion vom Grad $n-1$.

Dieser Satz lässt sich folgendermaßen beweisen:
Sei $x_0$ eine Nullstelle von f(x). Angenommen durch Polynomdivision erhält man $f(x)=(x-x_0)\cdot g(x)+r$, also mit einem Rest r, der nicht von x abhängt.
Lässt man nun die Werte von x gegen $x_0$ streben, dann erhält man $f(x_0)=r$.
Da $x_0$ nach Voraussetzung eine Nullstelle von f(x) ist, gilt auch auf $f(x_0)=0$.
Damit ist $r=0$, d.h., die Polynomdivision ist ohne Rest ausführbar.
Mit g(x) kann man wiederum so verfahren. Bei jedem Schritt verringert sich der Grad des verbleibenden Polynoms jeweils um 1, d.h., es kann höchstens n Linearfaktoren geben. Es gilt also der Satz:

• Eine ganzrationale Funktion $f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\mathrm{...}+a_{1}x+a_0$ vom Grad n (mit $n\in \mathbb{N}$), hat höchstens n Nullstellen.

Lässt sich aus der ganzrationalen Funktion f(x) der Linearfaktor $\left(x-x_0\right)$ mehrfach, etwa k-fach, ausklammern, so nennt man $x_0$ mehrfache Nullstelle (man nennt k auch die Ordnung der Nullstelle). Dabei lassen sich folgende Fälle unterscheiden:

1. $k=1$
   $x_0$ ist eine einfache Nullstelle; der Graph der Funktion schneidet an dieser Stelle die x-Achse.
2. $k>1$ und k gerade
   $x_0$ ist eine k-fache Nullstelle; der Graph der Funktion berührt die x-Achse (die 1. Ableitung an der Stelle $x_0$ ist gleich null).
3. $k>1$ und k ungerade
   $x_0$ ist eine k-fache Nullstelle; der Graph schneidet die x-Achse $\left(f\text{'}\left(x_0\right)\ne 0\right)$.

Hat eine ganzrationale Funktion n-ten Grades $f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\mathrm{...}+a_{1}x+a_0$ die Nullstellen $x_1,x_2,\mathrm{...,}{x}_n$, so kann man sie nach dem Nullstellensatz für Polynome, einem fundamentalen Satz der Algebra, folgendermaßen als Produkt aus Linearfaktoren darstellen:
$f(x)=a_n\left(x-x_1\right)\cdot \left(x-x_2\right)\cdot \mathrm{...}\cdot \left(x-x_n\right)$

Eine wichtige Hilfe bei der Zerlegung einer ganzrationalen Funktion in ihre Linearfaktoren ist folgender Satz:

• Wenn eine ganzrationale Funktion $f(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\mathrm{...}+a_{1}x+a_0$ mit $a_i\in \mathbb{Z}$ gegeben ist, so ist jede ganzzahlige Nullstelle $x_0$ ein Teiler vom Absolutglied $a_0$.

• Beispiel 3: Es sind alle Nullstellen der Funktionen f mit
  a) $f\left(x\right)=\left(x-2\right)\left(x+1\right)\left(x+3\right)\left(x+\mathrm{2,5}\right)$
  b) $f\left(x\right)=\left(x-1\right)\left(x+\mathrm{1,5}\right)\left(x^2+1\right)$
  zu bestimmen.

Lösung der Teilaufgabe a):
Der Funktionsterm ist bereits in Linearfaktoren zerlegt.
Man liest als Nullstellen sofort ab:
$x_1=2;x_2=-1;x_3=-3;x_4=-\mathrm{2,5}$

Lösung der Teilaufgabe b):
Die (unmittelbar ablesbaren) Nullstellen sind $x_1=1$ und $x_2=-\mathrm{1,5}$. Weitere Nullstellen gibt es nicht, da die aus dem dritten Faktor folgende Gleichung $x^2+1=0$ keine reelle Lösung besitzt.

• Beispiel 4: Von der Funktion $f\left(x\right)=x^5+6x^4+3x^3-10x^2$ sollen die Nullstellen berechnet werden.

Durch Nullsetzen und Ausklammern erhält man:
$\begin{array}{l}{x}^5+6x^4+3x^3-10x^2=0\\ x^2\left(x^3+6x^2+3x-10\right)=0\end{array}$

Aus $x^2=0$ folgt die zweifache Nullstelle $x_1=0$.
Weitere Nullstellen liefert die Gleichung $x^3+6x^2+3x-10=0$.
Als Teiler des Absolutgliedes kommen $\pm \mathrm{1,}\pm \mathrm{2,}\pm 5$ und $\pm 10$ in Frage.
Man überzeugt sich sehr schnell, dass $x_2=1$ die Bedingung erfüllt.
Division durch den Linearfaktor $\left(x-1\right)$ ergibt:
$\left(x^3+6x^2+3x-10\right):\left(x-1\right)=x^2+7x+10$

Die Lösungen der quadratischen Gleichung $x^2+7x+10=0$ sind die restlichen Nullstellen, also $x_3=-2$ und $x_4=-5$. Das heißt, die gegebene Funktion hat vier Nullstellen; ihre Zerlegung in Linearfaktoren ist:
$\begin{array}{l}f\left(x\right)=x\cdot x\cdot \left(x-1\right)\left(x+2\right)\left(x+5\right)\\ f\left(x\right)=x^2\cdot \left(x-1\right)\left(x+2\right)\left(x+5\right)\end{array}$

• Beispiel 5: Von einer ganzrationalen Funktion vierten Grades kennt man die Nullstellen $x_1=-\mathrm{2,}{x}_2=\mathrm{0,}{x}_3=\mathrm{3,}{x}_4=5$. Weiter sei $f\left(4\right)=-24$. Wie lautet die Funktionsgleichung?

Nach dem Nullstellensatz gilt:
$f\left(x\right)=a_4\cdot \left(x+2\right)\cdot x\cdot \left(x-3\right)\left(x-5\right)$
Mit $f\left(4\right)=-24$ erhält man daraus $a_4=1$ und somit die folgende Funktion:
$f\left(x\right)=\left(x+2\right)x\left(x-3\right)\left(x-5\right)=x^4+4x^3-x^2+30x$

• Beispiel 6: Die Nullstellen der Funktion $f\left(x\right)=x^2+2x-3$ sind zu ermitteln.

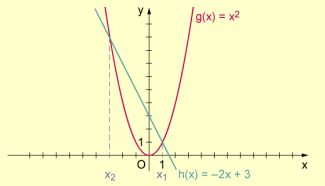
Aus $x^2+2x-3=0$ folgt $x^2=-2x+3$, d.h., der Funktionsterm von f ist auf diese Art und Weise geschickt in zwei Terme zerlegt worden, die wiederum Funktionen darstellen und deren Graphen man besonders einfach zeichnen kann (Normalparabel und Gerade). Die x-Koordinaten der Schnittpunkte der Graphen sind die Nullstellen der Ausgangsfunktion, denn nach den vorgenommenen Veränderungen gilt $f\left(x\right)=g\left(x\right)-h\left(x\right)$.
In diesem Fall liest man $x_1=-3$ und $x_2=1$ als Nullstellen ab (siehe Abbildung).

Zusammenfassung

Nullstellen ganzrationaler Funktionen ermittelt man rechnerisch durch

1. Anwenden der äquivalenten Umformungsregeln für Gleichungen;
2. Verwenden der Lösungsformel für quadratische Gleichungen;
3. Lösen durch Ausklammern und Substitution;
4. Vermuten von Nullstellen durch Auffinden der Teiler des Absolutgliedes und Faktorisieren der Funktion (Polynomdivision; schrittweises Verringern des Funktionsgrades um 1);
5. Anwenden von Näherungsverfahren;

bzw. grafisch durch

1. Zeichnen des Graphen der Funktion und Ablesen der Nullstellen an den Schnittpunkten des Graphen mit der x-Achse;
2. geschicktes Zerlegen des Funktionsterms von $f\left(x\right)$ in Funktionsterme $g\left(x\right)$ und $h\left(x\right)$ mit $f\left(x\right)=g\left(x\right)-h\left(x\right)$ (die x-Koordinaten der Schnittpunkte der Graphen von $g\left(x\right)$ und $h\left(x\right)$ sind dann die Nullstellen von $f\left(x\right)$).