Rechengesetze für Vektoren

Beim Vergleichen und beim Verknüpfen von Vektoren muss darauf geachtet werden, dass die Koordinatenanzahl, d.h. die Anzahl der Zeilen bei Darstellung als Spaltenvektor, übereinstimmt.
Für beliebige (n-dimensionale) Vektoren sind eine Addition sowie eine Vervielfachung mit reellen Zahlen definiert. Spezielle Produkte von Vektoren sind das Skalarprodukt sowie im dreidimensionalen Raum das Vektorprodukt und das Spatprodukt. Die Ergebnisse dieser Verknüpfungen können mithilfe der Koordinaten der zu verknüpfenden Vektoren berechnet werden.

Gleichheit von Vektoren (Prinzip des Koordinatenvergleichs)

Zwei Vektoren
$\vec{a} = (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix})$
sind genau dann gleich, wenn sie jeweils in ihren Koordinaten übereinstimmen, wenn also $a_{i} = b_{i} (f ü r i = 1, 2, ..., n)$ gilt.

Addition von Vektoren

Für die Summe zweier Vektoren
$\vec{a} = (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix})$
gilt:
$\vec{a} + \vec{b} = (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) + (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix}) = (\begin{matrix} a_{1} + b_{1} \\ a_{2} + b_{2} \\ ... \\ a_{n} + b_{n} \end{matrix})$

Die Addition von Vektoren ist kommutativ und assoziativ.

Beweis der Kommutativität:

$\begin{matrix} \vec{a} + \vec{b} = (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) + (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix}) = (\begin{matrix} a_{1} + b_{1} \\ a_{2} + b_{2} \\ ... \\ a_{n} + b_{n} \end{matrix}) \\ = (\begin{matrix} b_{1} + a_{1} \\ b_{2} + a_{2} \\ ... \\ b_{n} + a_{n} \end{matrix}) = (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix}) + (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) = \vec{b} + \vec{a} w . z . b . w . \end{matrix}$

Die Assoziativität kann sowohl durch Rückführung der Addition von Vektoren auf die Addition ihrer Koordinaten, die assoziativ ist, nachgewiesen oder wie in der folgenden Abbildung dargestellt veranschaulicht werden.

Addition von Vektoren (Assoziativgesetz)

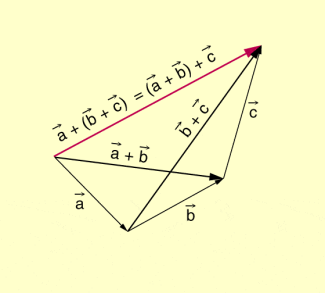
Beispiel:
$(\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) + (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix}) = (\begin{matrix} 3 \\ 3 \\ 7 \end{matrix})$

Subtraktion von Vektoren

Die Subtraktion von Vektoren lässt sich auf die Addition zurückführen.
Ein Vektor $\vec{b}$ wird von einem Vektor $\vec{a}$ subtrahiert, indem man den zu $\vec{b}$ entgegengesetzten Vektor $- \vec{b}$ (mit dem umgekehrten Vorzeichen aller Koordinaten) zu $\vec{a}$ addiert:
$\vec{a} - \vec{b} = \vec{a} + (- \vec{b}) = (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) + (\begin{matrix} - b_{1} \\ - b_{2} \\ ... \\ - b_{n} \end{matrix}) = (\begin{matrix} a_{1} + (- b_{1}) \\ a_{2} + (- b_{2}) \\ ... \\ a_{n} + (- b_{n}) \end{matrix}) = (\begin{matrix} a_{1} - b_{1} \\ a_{2} - b_{2} \\ ... \\ a_{n} - b_{n} \end{matrix})$

Subtraktion von Vektoren

Multiplikation (Vervielfachung) eines Vektors mit einer Zahl

Für die Multiplikation (Vervielfachung) eines Vektors mit einer reellen Zahl (einem Skalar) gilt:
$r \vec{a} = (\begin{matrix} r a_{1} \\ r a_{2} \\ ... \\ r a_{n} \end{matrix}) (r \in ℝ)$

Anmerkung: Für den Fall, dass mit einer natürlichen Zahl n multipliziert werden soll, lässt sich die Vielfachbildung auf die Addition von Vektoren zurückführen.

Beispiel: Es sei $r = 2, s = 3, {\vec{a}}^{T} = (\begin{matrix} 2 & 5 & 3 \end{matrix}) u n d {\vec{b}}^{T} = (\begin{matrix} 1 & - 2 & 4 \end{matrix}) .$

In der folgenden Tabelle sind einige Gesetzmäßigkeiten der Vielfachbildung angegeben und anhand des obigen Beispiels „nachgewiesen“.

Gesetzmäßigkeit	Beispiel
$r (s \vec{a}) = (r s) \vec{a}$	$2 (3 (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix})) = 2 (\begin{matrix} 6 \\ 15 \\ 9 \end{matrix}) = (\begin{matrix} 12 \\ 30 \\ 18 \end{matrix}) = 6 (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) = (\begin{matrix} 12 \\ 30 \\ 18 \end{matrix})$
$(r + s) \vec{a} = r \vec{a} + s \vec{a}$	$(2 + 3) (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) = 5 (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) = (\begin{matrix} 10 \\ 25 \\ 15 \end{matrix}) = 2 (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) + 3 (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) = (\begin{matrix} 4 \\ 10 \\ 6 \end{matrix}) + (\begin{matrix} 6 \\ 15 \\ 9 \end{matrix}) = (\begin{matrix} 10 \\ 25 \\ 15 \end{matrix})$
$r (\vec{a} + \vec{b}) = r \vec{a} + r \vec{b}$	$2 ((\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) + (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix})) = 2 (\begin{matrix} 3 \\ 3 \\ 7 \end{matrix}) = (\begin{matrix} 6 \\ 6 \\ 14 \end{matrix}) = 2 (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) + 2 (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix}) = (\begin{matrix} 4 \\ 10 \\ 6 \end{matrix}) + (\begin{matrix} 2 \\ - 4 \\ 8 \end{matrix}) = (\begin{matrix} 6 \\ 6 \\ 14 \end{matrix})$

Produkte von Vektoren

Für das Skalarprodukt $\vec{a} \cdot \vec{b}$ zweier Vektoren
$\vec{a} = (\begin{matrix} a_{1} \\ a_{2} \\ ... \\ a_{n} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{1} \\ b_{2} \\ ... \\ b_{n} \end{matrix})$
gilt:
$\vec{a} \cdot \vec{b} = a_{1} b_{1} + a_{2} b_{2} + ... + a_{n} b_{n} = \sum_{i = 1}^{n} a_{i} b_{i}$
Das Ergebnis dieser (skalaren) Multiplikation von Vektoren ist eine reelle Zahl, ein Skalar.

Beispiel:
$(\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) \cdot (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix}) = 2 \cdot 1 + 5 \cdot (- 2) + 3 \cdot 4 = 2 - 10 + 12 = 4$

Anmerkung: Das Skalarprodukt $\vec{a} \cdot \vec{b}$ kann auch als $\vec{a} \cdot \vec{b} = | \vec{a} | \cdot | \vec{b} | \cdot \cos ∢ (\vec{a}; \vec{b})$ berechnet werden.

Für das Vektorprodukt zweier Vektoren
$\vec{a} = (\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}) u n d \vec{b} = (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix})$
im dreidimensionalen Raum gilt:
$\vec{a} \times \vec{b} = (\begin{matrix} a_{2} b_{3} - a_{3} b_{2} \\ a_{3} b_{1} - a_{1} b_{3} \\ a_{1} b_{2} - a_{2} b_{1} \end{matrix})$
Das Ergebnis dieser (vektoriellen) Multiplikation ist wieder ein Vektor.

Beispiel:
$(\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) \times (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix}) = (\begin{matrix} 5 \cdot 4 - 3 \cdot (- 2) \\ 3 \cdot 1 - 2 \cdot 4 \\ 2 \cdot (- 2) - 5 \cdot 1 \end{matrix}) = (\begin{matrix} 26 \\ - 5 \\ - 9 \end{matrix})$

Der Betrag des Vektorproduktes $| \vec{a} \times \vec{b} |$ ist gleich der Maßzahl des Inhalts des von den beiden Vektoren aufgespannten Parallelogramms mit folgender Berechnungsmöglichkeit:
$| \vec{a} \times \vec{b} | = | \vec{a} | \cdot | \vec{b} | \cdot \sin ∢ (\vec{a}; \vec{b})$

Für das Spatprodukt von drei Vektoren
$\vec{a} = (\begin{matrix} a_{1} \\ a_{2} \\ a_{3} \end{matrix}); \vec{b} = (\begin{matrix} b_{1} \\ b_{2} \\ b_{3} \end{matrix}) u n d \vec{c} = (\begin{matrix} c_{1} \\ c_{2} \\ c_{3} \end{matrix}) .$
gilt:
$(\vec{a} \times \vec{b}) \cdot \vec{c} = | \begin{matrix} a_{1} & b_{1} & c_{1} \\ a_{2} & b_{2} & c_{2} \\ a_{3} & b_{3} & c_{3} \end{matrix} |$

Für $(\vec{a} \times \vec{b}) \cdot \vec{c} = 0$ liegen die Vektoren in einer Ebene, sind also linear abhängig.

Beispiel: Es sei $\vec{a} = (\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}), \vec{b} = (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix}) u n d \vec{c} = (\begin{matrix} 0 \\ 1 \\ 2 \end{matrix}) .$

Dann gilt:
$(\vec{a} \times \vec{b}) \cdot \vec{c} = ((\begin{matrix} 2 \\ 5 \\ 3 \end{matrix}) \times (\begin{matrix} 1 \\ - 2 \\ 4 \end{matrix})) \cdot (\begin{matrix} 0 \\ 1 \\ 2 \end{matrix}) = (\begin{matrix} 26 \\ - 5 \\ - 9 \end{matrix}) \cdot (\begin{matrix} 0 \\ 1 \\ 2 \end{matrix}) = - 23$
Geometrische Interpretation: Das Spatprodukt ist betragsmäßig gleich dem Volumen des durch die drei Vektoren aufgespannten Parallelepipeds (Spats).

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Rechengesetze für Vektoren

Gleichheit von Vektoren (Prinzip des Koordinatenvergleichs)

Addition von Vektoren

Subtraktion von Vektoren

Multiplikation (Vervielfachung) eines Vektors mit einer Zahl

Produkte von Vektoren

Rechtliches

Einloggen