Spatprodukt von drei Vektoren des Raumes
Die Betrachtung eines Anwendungsbeispiels führt in Analogie zum Skalar- bzw. Vektorprodukt zur Einführung eines neuen Produktes für drei Vektoren, dem Spatprodukt.
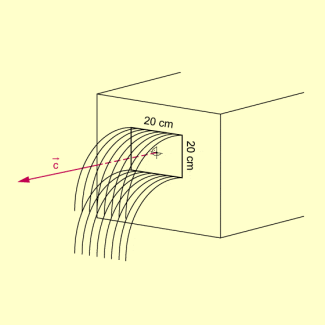
Aus einer quadratischen Öffnung mit einer Kantenlänge von 20 cm ströme Wasser mit einer Geschwindigkeit von 3 senkrecht aus. Es ist nach der Wassermenge gefragt, die pro Sekunde aus dieser Öffnung austritt. Dabei wird die Fließgeschwindigkeit des Wassers als eine vektorielle Größe aufgefasst, die durch den Vektor gekennzeichnet wird.
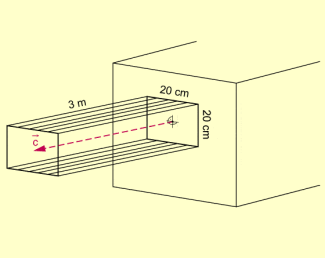
Um diese Wassermenge zu bestimmen, kann man sich vorstellen, dass das ausströmende Wasser in einer Sekunde einen Quader mit quadratischer Grundfläche (Kantenlänge 20 cm) und einer Höhe von 3 m füllt.
Das Volumen dieses Quaders beträgt demzufolge 0,2 m · 0,2 m · 3 m = .
Folglich strömt aus der Öffnung Wasser, was entspricht.
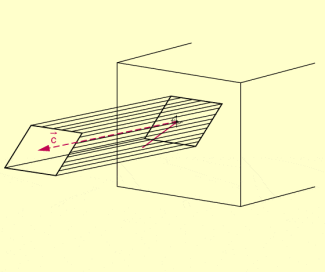
Nun tritt das Wasser aus einer Öffnung aus, die nicht mehr quadratisch ist, aber der Form eines Parallelogramms entspricht. Darüber hinaus nehmen wir an, dass das Wasser nicht mehr senkrecht aus dieser Öffnung ausströmt.
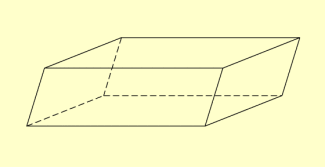
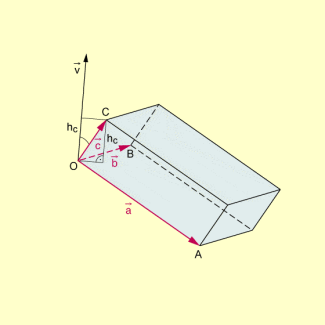
Die ausgetretene Wassermenge füllt damit in der betrachteten Zeiteinheit einen Körper, der durch sechs Parallelogramme begrenzt wird. Es handelt sich dabei um ein Prisma mit einem Parallelogramm als Grundfläche. Ein solcher Körper heißt auch Parallelepiped oder Spat.
In der Natur kommt diese Körperform z.B. in der kristallinen Form des Flussspates vor.
Dieser Körper ist eindeutig durch drei linear unabhängige Vektoren bestimmt.
Das Volumen eines solchen Parallelepipeds lässt sich mit berechnen. Dabei bedeutet die Größe der Grundfläche, also des Parallelogramms, welches durch aufgespannt wird, und es gilt entsprechend der geometrischen Interpretation des Vektorprodukts:
Es sei die Länge der Höhe von C über der betrachteten Grundfläche.
Bezeichnet den Winkel zwischen den beiden Vektoren , so gilt .
Damit erhält man aber insgesamt bzw. (entsprechend der Definition des Skalarprodukts).
Weil sowohl positiv als auch negativ sein kann, ist das hier berechnete Volumen eine vorzeichenbehaftete Größe.
Es ist positiv, wenn die drei Vektoren ein Rechtssystem bilden und negativ im anderen Fall.
In Analogie zum Skalar- bzw. Vektorprodukt nutzen wir die an obigem Beispiel betrachteten Beziehungen zur Einführung eines neuen Produktes für drei Vektoren:
- Definition: Sind Vektoren, so bezeichnet das Spatprodukt dieser drei Vektoren.
Das Produkt gibt das (vorzeichenbehaftete) Volumen des Spats (Parallelepipeds) an, das durch die drei Vektoren bestimmt ist (vergleiche mit der letztgenannten Abbildung).
Es ist damit auch klar, dass gilt, wenn einer der drei Vektoren der Nullvektor ist.
Sind alle drei Vektoren vom Nullvektor verschieden, dann ist genau dann, wenn linear abhängig (also komplanar) sind. Diese Beziehung lässt sich benutzen, um festzustellen, ob vier Punkte in einer Ebene liegen. Es gilt der folgende Satz:
- Komplanaritätskriterium für vier Punkte einer Ebene
Sind A, B, C und D vier voneinander verschiedene Punkte im Raum, so liegen diese vier Punkte genau dann in einer gemeinsamen Ebene, wenn gilt.
Aus der geometrischen Interpretation des Spatprodukts (vergleiche wieder mit der letztgenannten Abbildung) ist erkennbar, dass gilt.
Aus diesem Grunde kann man das Spatprodukt der drei Vektoren auch in der Form schreiben.
Das Spatprodukt besitzt außerdem die folgenden Eigenschaften:
Nun soll das Spatprodukt berechnet werden, wenn die drei Vektoren durch ihre Koordinaten gegeben sind.
Mit
= , = und =
erhält man
Diese Summe lässt sich als die folgende, nach der letzten Spalte entwickelte Determinante auffassen:
Zusammenfassend lässt sich feststellen und als Satz formulieren:
- Spatprodukt von drei Vektoren
Sind die drei Vektoren
=, = und =
gegeben, so lässt sich deren Spatprodukt durch
berechnen.