Totale Wahrscheinlichkeit
Mitunter wird man mit dem Problem konfrontiert, die Wahrscheinlichkeit für ein Ereignis A zu berechnen, das im Zusammenhang mit n verschiedenen Ereignissen auftritt (in der Praxis können die zum Beispiel verschiedene Fälle oder Ursachen von A sein), wobei sich die Wahrscheinlichkeiten für die Ereignisse und insbesondere für das Eintreten von A unter der Bedingung, dass jeweils ein eingetreten ist, mitunter leichter angeben bzw. ermitteln lassen.
Gesucht ist also eine Aussage über eine „unbedingte“ Wahrscheinlichkeit, wenn Informationen über bedingte Wahrscheinlichkeiten vorliegen bzw. primär bestimmbar sind. Bei einer solchen Problemsituation wird man versuchen, den im Folgenden angeführten Satz der totalen Wahrscheinlichkeit anzuwenden.
- Bilden die Ereignisse eine Zerlegung von , d.h. besitzen die Ereignisse die Eigenschaften
so gilt:
Die Gültigkeit dieser Aussage kann man leicht veranschaulichen.
-
Veranschaulichung zum Satz der totalen Wahrscheinlichkeit
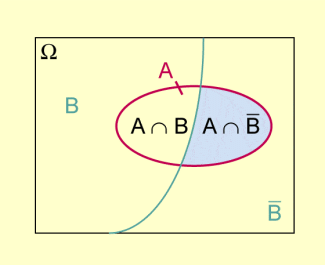
Der Einfachheit halber wählen wir als Zerlegung von die Ereignisse B und mit positiver Wahrscheinlichkeit.
Dann gilt und somit
aufgrund der Additivität von P, da ist.
Aufgrund des Multiplikationssatzes und folgt dann:
Anmerkung: Die Bezeichnung totale (oder volle bzw. vollständige) Wahrscheinlichkeit nimmt Bezug auf den Sachverhalt, dass aus den bedingten Wahrscheinlichkeiten eines Ereignisses A die unbedingte (totale ...) Wahrscheinlichkeit berechnet werden kann.
Die Gegebenheiten des Satzes der totalen Wahrscheinlichkeit können auch als zweistufiger Vorgang aufgefasst werden, wobei auf der ersten Stufe die Bedingungen und auf der zweiten Stufe das Ereignis A beobachtet werden. Man kann den Sachverhalt mithilfe eines Baumdiagramms veranschaulichen, der Satz der totalen Wahrscheinlichkeit erweist sich dann als ein Spezialfall der zweiten Pfadregel.
-
Baumdiagramm zum Satz der totalen Wahrscheinlichkeit
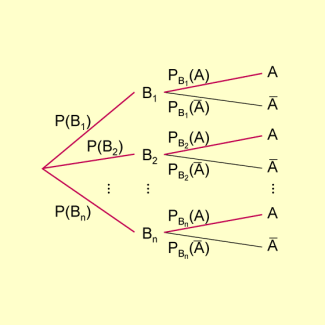
Der hier angegebene Satz der totalen Wahrscheinlichkeit lässt sich wie folgt verallgemeinern:
- Die Zerlegung von kann aus abzählbar unendlich vielen Ereignissen bestehen. Es gilt dann:
- Der Satz der totalen Wahrscheinlichkeit kann auch benutzt werden, wenn mehrere Zerlegungen vorliegen, d.h., wenn der entsprechende Vorgang als ein mehrstufiger Vorgang aufgefasst werden kann. Wählt man der Einfachheit halber auf der ersten Stufe die Zerlegung B und und auf der zweiten Stufe eine Zerlegung C und , so erhält man:
-
Anwendung des Satzes der totalen Wahrscheinlichkeit bei einem mehrstufigen Vorgang
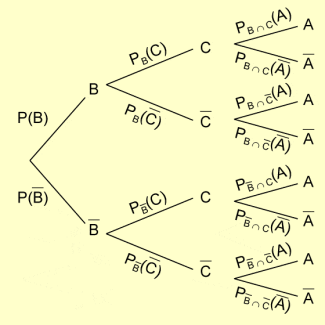
Wir betrachten zur Anwendung des Satzes der totalen Wahrscheinlichkeit das folgende Beispiel:
Beispiel: Ein Unternehmen, das großen Wert auf seinen guten Ruf legt, strebt an, dass kein von ihm produziertes Gerät das Werk verlässt, das unbrauchbar ist. Dazu verwendet man ein kostengünstiges Prüfverfahren, das allerdings keine hundertprozentig richtigen Aussagen darüber liefert, ob ein kontrolliertes Gerät tatsächlich unbrauchbar ist oder nicht. bezeichne das Ereignis, dass ein hergestelltes Gerät brauchbar ist, und das Ereignis, dass ein kontrolliertes Gerät als brauchbar eingestuft wird. Zur Fundierung der Unternehmensstrategie möchte man den mittleren Anteil der durch das Prüfverfahren als unbrauchbar eingestuften und damit nicht zur Auslieferung kommenden Geräte kennen.
Wir gehen zur Lösung des Problems von folgenden fiktiven (auf Erfahrungswerten beruhenden) Angaben aus:
Mithilfe des Satzes der totalen Wahrscheinlichkeit erhält man:
Obwohl im Durchschnitt nur 6 von 100 Geräten nach der Produktion tatsächlich unbrauchbar sind, werden durch das Prüfverfahren etwa 12 Geräte als solche eingestuft.
Wie dieses Ergebnis ökonomisch zu bewerten ist, würde von einem Kostenvergleich abhängen. Sollte man als „Unternehmer“ mit diesem Resultat unzufrieden sein, so können verschiedene Veränderungsmöglichkeiten durchgespielt werden, wie zum Beispiel:
- eine Verbesserung der Produktion, d.h. eine Vergrößerung von ;
- die Verwendung eines Prüfverfahrens, das unbrauchbare Geräte besser als solche identifiziert, d.h. eine Vergrößerung von ;
- den Einsatz eines Prüfverfahrens, das brauchbare Geräte besser als solche identifiziert, d.h. eine Vergrößerung von .
Erstrebenswert wäre natürlich ein vollständiges Überprüfen der produzierten Geräte. Das ist aber oftmals sehr teuer oder sehr zeitaufwendig oder auch gar nicht möglich.

