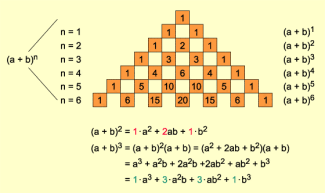Binome
Zweigliedrige Ausdrücke, sogenannte Binome, nehmen wegen ihres häufigen Auftretens in der Mathematik einen besonderen Platz ein.
Dabei sind Potenzen von Binomen von großem Interesse.
Wenn a, b und n natürliche Zahlen sind, gilt folgende Beziehung, die auch binomischer Satz genannt wird:
Zweigliedrige Ausdrücke, sogenannte Binome nehmen wegen ihres häufigen Auftretens in der Mathematik einen besonderen Platz ein.
Dabei sind Potenzen von Binomen von großem Interesse.
Wenn a, b und n natürliche Zahlen sind, gilt folgende Beziehung, die auch binomischer Satz genannt wird:
Die Ausdrücke (gesprochen: n über k) heißen Binominalkoeffizienten und sind wie folgt definiert:
Für das Produkt aller natürlichen Zahlen von 1 bis m schreibt man auch m!.
Also
-
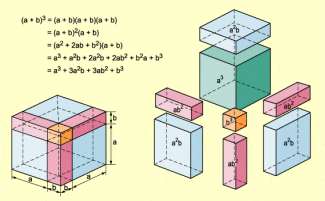
Geometrische Veranschaulichung der dritten Potenz von (a + b)
Damit vereinfacht sich der Binominalkoeffizient n über k, und es gilt:
Beispiel:
Binominalkoeffizienten spielen in der Kombinatorik eine wichtige Rolle.
Der binomische Satz lässt sich erweitern, indem als Exponenten beliebige reelle Zahlen zugelassen werden.
Setzt man dann a = 1 und b = x erhält man die sogenannte binomische Reihe
Diese Reihe konvergiert wenn der Betrag von x kleiner 1 ist, d. h. die Summe nähert sich einem bestimmten Wert (Grenzwert).
Aus dieser Reihe lassen sich Näherungsformeln ableiten, z. B.:
(für hinreichend kleine Werte von x)
Die Binominalkoeffizienten ergeben sich auch aus dem pascalschen Dreieck. Diese pyramidenförmige Anordnung von Zahlen, bei der eine 1 an der Spitze steht und jede neue Zeile mit 1 beginnt und mit 1 endet und bei der in den Lücken jeweils die Summe der darüber stehenden Zahlen steht, wurde zwar nach BLAISE PASCAL benannt, war aber schon früher bekannt.
So beschrieb der chinesische M athematiker CHU SHIH CHIEM 1303 eine solche Anordnung. In Europa finden sie sich bei MICHAEL STIFEL, NICCOLÒ TARTAGLIA und GERONIMO CARDANO. Sie wurden von diesen Mathematikern zum Berechnen höherer Potenzen verwandt.
-
Pascalsches Dreieck