Bogenmaß

Zwischen der Größe des Winkels $\alpha$ eines Kreissektors und der Länge b des zugehörigen Bogens besteht eine umkehrbar eindeutige Beziehung. Bezeichnet u die Länge des Umfangs des gesamten Kreises (mit dem Radius r), so gilt:
$b:u=\alpha :360°$
Mit $u=2\pi \cdot r$ folgt hieraus:
$b:2\pi r=\alpha :360°$
bzw.
$b=\frac{\pi }{180°}r\cdot \alpha$
Bildet man nun das Verhältnis $\frac{b}{r}$, so ist dies wegen $\frac{b}{r}=\frac{\pi }{180°}\cdot \alpha$ nur von der Größe des Winkels $\alpha$ abhängig. Zu jedem Winkel $\alpha$, dessen Größe in Gradmaß angegeben ist, gehört also ein eindeutig bestimmter Wert des Verhältnisses $\frac{b}{r}$, der sich mittels $\frac{\pi }{180°}\cdot \alpha$ berechnen lässt. Das gilt auch für Winkel, die kleiner als 0° oder größer als 360° sind. Wegen dieser eindeutigen Beziehung kann man die reelle Zahl $\alpha \cdot \frac{\pi }{180°}$ als ein weiteres Maß für die Größe eines Winkels $\alpha$ verwenden. Man nennt es das Bogenmaß des Winkels $\alpha$.

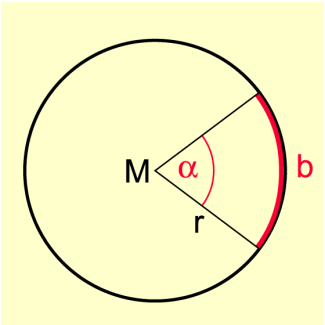
Das Bogenmaß eines Winkels $\alpha$ ist das Verhältnis (der Länge) des zu diesem Winkel gehörenden Kreisbogens b und (der Länge) des Kreisradius r. Es wird mit arc $\alpha$ (gesprochen: arkus alpha) oder $\stackrel{⌢}{\alpha }$ bezeichnet (arcus (lat.) – Bogen):
$arc\alpha =\frac{b}{r}=\frac{\pi }{180°}\cdot \alpha$

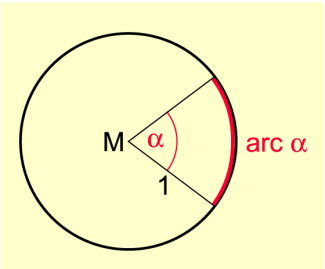
Am Einheitskreis ist wegen r = 1 (Längeneinheit)
$arc\alpha =b$. Deshalb kann man auch in folgender Weise formulieren:

Das Bogenmaß eines Winkels $\alpha$ ist die Maßzahl der Länge des zu diesem Winkel gehörenden Kreisbogens b auf dem Einheitskreis.

Die Einheit des Bogenmaßes beim Messen der Größe von Winkeln ist 1 Radiant (1 rad).
1 rad ist also die Größe des Winkels, für den der Bogen auf dem Einheitskreis die Länge 1 (LE) besitzt. Aus $1rad=\frac{\pi }{180°}\cdot \alpha$ folgt:
$\alpha =1\cdot \frac{180°}{\pi }\approx \mathrm{57,295}78°(bzw.57°17⏢\text{45")}$.
Umgekehrt gilt:
$1°=\frac{\pi }{180°}rad\approx \mathrm{0,01}7453rad$

Bei der Angabe von Winkelgrößen in Bogenmaß wird auf die Einheit rad meist verzichtet und lediglich die entsprechende reelle (Maß-)Zahl angegeben – also z. B. $1°=\mathrm{0,01}7453$.
Häufig gibt man das Bogenmaß als ganzzahliges oder gebrochenes Vielfaches von $\pi$ an.