- Lexikon
- Mathematik
- 6 Funktionen
- 6.3 Lineare Funktionen
- 6.3.2 Funktionen mit der Gleichung y = m · x + n
- Funktionsgleichung, Ermitteln
Funktionsgleichung, Ermitteln
Eine lineare Funktion ist durch zwei ihrer Wertepaare bzw. durch zwei Punkte ihres Graphen eindeutig bestimmt.
Ist eines des gegebenen Wertepaare das Paar (0; 0), verläuft der Graph der Funktion also durch den Koordinatenursprung, so ist das Ermitteln der Gleichung besonders einfach.
1. Weg:
Da der Graph die y-Achse an der Stelle 0 schneidet, hat der Parameter n in der Gleichung den Wert null. Es gilt also und damit . Mithilfe der Koordinaten (x; y) eines zweiten gegebenen Punktes des Graphen lässt sich damit m berechnen, da diese Koordinaten die Gleichung erfüllen müssen.
Beispiele:
Der Graph einer lineare Funktion verlaufe
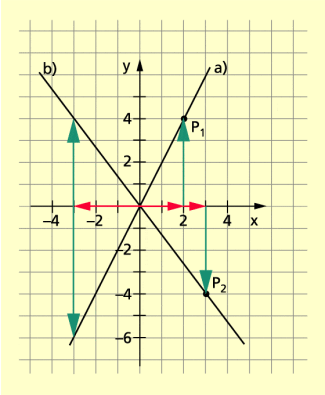
a) durch den Koordinatenursprung und den Punkt ;
b) durch den Koordinatenursprung und den Punkt .
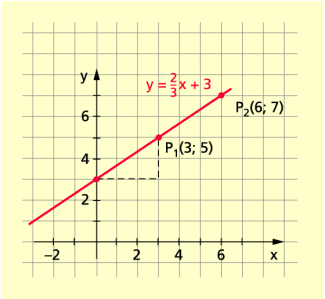
Es ist jeweils die Gle ichung der Funktion aufzustellen (Bild 1).
a) Aus folgt . Damit gilt:
b) Aus folgt . Damit gilt:
Graphen durch den Koordinatenursprung
2. Weg:
Wir tragen in den durch die zwei Punkte gegebenen Graphen der Funktion ein Anstiegsdreieck ein und berechnen aus dessen Kathetenlängen (zumindest näherungsweise) das Verhältnis .
Bezogen auf obige Beispiele ergibt sich somit aus dem Bild 1:
a)
b)
Der durch zwei Punkte eindeutig bestimmte Graph einer linearen Funktion verlaufe nicht durch den Koordinatenursprung.
Beispiel:
und seien zwei Punkte des Graphen der linearen Funktion y = f(x) = mx + n. Es ist die Gleichung der Funktion aufzustellen.
1. Weg:
Aus dem Bild 2 ist zu entnehmen, dass die Gerade die y-Achse an der Stelle 2 schneidet. Also ist n = 2 und damit . Der Wert von m kann wiederum unter Verwendung der Kathetenlängen eines Anstiegsdreiecks ermittelt werden. In unserem Fall gilt:
Auch eine andere Überlegung ist möglich: Die Koordinaten von (und auch von ) müssen die Gleichung von f erfüllen. Es gilt also , woraus man ebenfalls erhält.
Die Gleichung der Funktion f lautet somit y = f(x) = x + 2.
y=23x+ 2
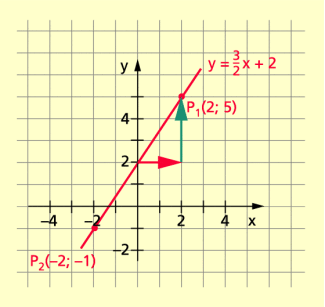
2. Weg:
Die Koordinaten von und von müssen die Gleichung
y = mx + n erfüllen.
in y = mx + n eingesetzt liefert:
I. 5 = 2m + n
in y = mx + n eingesetzt liefert:
II. –1 = –2m + n
Man erhält ein lineares Gleichungssystem, das z. B. durch das Additionsverfahren gelöst werden kann:
Antwort: ist die Funktionsgleichung.
Das im Beispiel dargestellte Verfahren, allgemein auf zwei Punkte
und angewandt, führt zu:
Subtrahiert man die zweite Gleichung von der ersten, um n zu eliminieren, so ergibt sich:
Allgemein: Ist f eine lineare Funktion mit dem Anstieg m, so gilt für
Mit diesem Satz kann der Anstieg m einer Funktion sofort ermittelt werden und lässt sich dann n errechnen.
Material zum Thema
Beispiel:
Gesucht: Funktionsgleichung
Gegeben:; als Punkte des Graphen einer linearen Funktion mit y = mx + n (Bild 3)
Lösung:
Werte z. B. von eingesetzt:
Antwort: ist die Funktionsgleichung.
y=23x+3
Ein Angebot von 