Hexadezimalsystem

Das Hexadezimalsystem verwendet als Basis die Zahl 16.
Damit werden 16 Grundziffern benötigt.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Jetzt 30 Tage risikofrei testen

Das Hexadezimalsystem verwendet als Basis die Zahl 16.
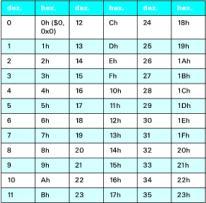
Damit werden 16 Grundziffern benötigt, 6 Ziffern mehr als beim Dezimalsystem. Für diese Ziffern werden Buchstaben verwendet:

A für 10, B für 11, C für 12, D für 13, E für 14 und F für 15

Dezimalsystem Zahlendarstellung	Hexadezimalsystem
$\begin{array}{l} 12 = 1 \cdot 10^{1} + 2 \cdot 10^{0} \\ 23 = 2 \cdot 10^{1} + 3 \cdot 10^{0} \\ 30 = 3 \cdot 10^{1} \\ 300 = 3 \cdot 10^{2} \\ 41743 = \\ 4 \cdot 10^{4} + 1 \cdot 10^{3} + 7 \cdot 10^{2} + 4 \cdot 10^{1} + 3 \cdot 10^{0} \end{array}$	$\begin{array}{l} C = 12 \cdot 16^{0} = 12 \\ 17 = 1 \cdot 16^{1} + 7 \cdot 16^{0} = 23 \\ 1 E = 1 \cdot 16^{1} + 14 \cdot 16^{0} = 30 \\ 12 C = 1 \cdot 16^{2} + 2 \cdot 16^{1} + 12 \cdot 16^{0} \\ = 256 + 32 + 12 = 300 \\ A 30 F = 10 \cdot 16^{3} + 3 \cdot 16^{2} + 0 \cdot 16^{1} + 15 \cdot 16^{0} \\ = 10 \cdot 4096 + 3 \cdot 256 + 15 \\ = 40960 + 768 + 15 = 41743 \end{array}$
Schriftliche Addition
$\begin{array}{l} 12 \\ 23 \\ 30 \\ \underline{300} \\ 365 \end{array}$	$\begin{array}{l} C \\ 17 \\ 1 E \\ \underline{12 C} \\ 16 D \\ E i n e r s t e l l e : 12 + 7 + 14 + 12 = 45, \\ s c h r e i b e 13 (45 - 32), m e r k e 2, (32 = 2 \cdot 16) \\ 16 e r - S t e l l e : 2 + 2 + 1 + 1 = 6, s c h r e i b e 6 \\ 256 e r - S t e l l e : 1, s c h r e i b e 1 \\ E r g e b n i s : 1 \cdot 256 + 6 \cdot 16 + 13 = 256 + 96 + 13 = 365 \end{array}$
Schriftliche Multiplikation
$\begin{array}{l} \underline{23 \cdot 30} \\ 690 \end{array}$	$\begin{array}{l} \underline{17 \cdot 1 E} \\ 142 \\ 17 \\ \bar{2B2} \\ E r s t e Z e i l e : 17 \cdot E = 17 \cdot 14 \\ 1. S t e l l e v o n r e c h t s : 7 \cdot 14 = 98, \\ s c h r e i b e 2 (98 - 96), m e r k e 6 (96 = 6 \cdot 16) \\ 2. S t e l l e v o n r e c h t s : 1 \cdot 14 + 6 = 20, s c h r e i b e 4 m e r k e 1, \\ 3. S t e l l e v o n r e c h t s : s c h r e i b e 1 \\ Z w e i t e Z e i l e : 17 \cdot 1 \\ 1. S t e l l e v o n r e c h t s : f r e i \\ 2. S t e l l e v o n r e c h t s : s c h r e i b e 7 \\ 3. S t e l l e v o n r e c h t s : s c h r e i b e 1 \\ A d d i t i o n : 2; 11 = B; 2 \\ E r g e b n i s : 2 \cdot 256 + 11 \cdot 16 + 2 = 512 + 176 + 2 = 690 \end{array}$

Lernhelfer (Duden Learnattack GmbH): "Hexadezimalsystem." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/hexadezimalsystem (Abgerufen: 20. May 2025, 04:48 UTC)

Suche nach passenden Schlagwörtern

Jetzt durchstarten

Entspannt durch die Schule mit KI-Tutor Kim und Duden Learnattack.

Kim hat in Deutsch, Mathe, Englisch und 6 weiteren Schulfächern immer eine von Lehrkräften geprüfte Erklärung, Video oder Übung parat.
24/7 auf Learnattack.de und WhatsApp mit Bildupload und Sprachnachrichten verfügbar. Ideal, um bei den Hausaufgaben und beim Lernen von Fremdsprachen zu unterstützen.
Viel günstiger als andere Nachhilfe und schützt deine Daten.

Hexadezimalsystem

Schule wird easy mit KI-Tutor Kim und Duden Learnattack

Suche nach passenden Schlagwörtern