Kegelschnitte
Reguläre Kegelschnitte entstehen, wenn die Mantelfläche eines geraden Kreiskegels (Doppelkegel) von einer Ebene geschnitten wird, die nicht durch die Spitze S des Kreiskegels geht. Je nach der Lage der Schnittebene unterscheidet man verschiedene Kegelschnittkurven: Ellipsen, Parabeln, Hyperbeln, Kreise.
Ist der Winkel zwischen der Kegelachse und den Mantellinien, so heißt 2 Öffnungswinkel des Kreiskegels. ist der Schnittwinkel zwischen der Schnittebene und der Achse des Doppelkegels.
Liegt die Schnittebene schräg zur Achse des Doppelkegels und verläuft sie nicht durch die Spitze, so unterscheidet man drei Fälle:
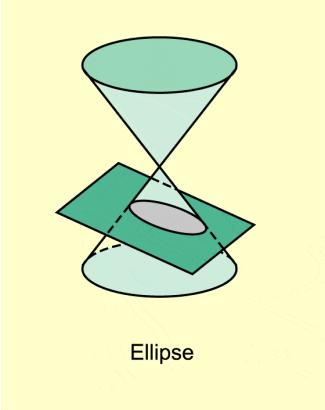
Gilt so ist die Kegelschnittkurve eine Ellipse.
Liegt die Schnittebene senkrecht zur Achse des Doppelkegels und geht sie nicht durch die Spitze des Kegels, so entstehen Kreise.
Ellipse
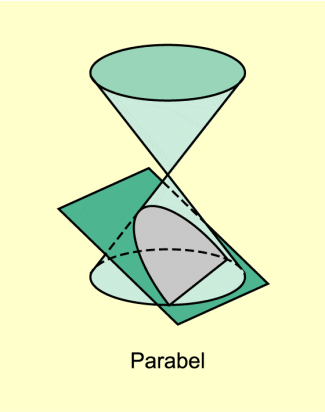
Gilt so ist die Kegelschnittkurv e eine Parabel.
Parabel
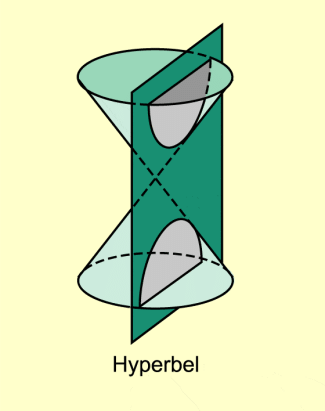
Gilt , so ist die Kegelschnittkurve eine Hyperbel.
Verläuft die Schnittkurve durch die Spitze der Doppelkegels, so enstehen für:
- der Punkt S der Kegelspitze
- eine Gerade (eine Mantellinie)
- zwei Geraden (zwei Mantellinien)
Hyperbel
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 