Logarithmen, Wissenswertes und Historisches

Die Logarithmengesetze lassen sich zum praktischen Rechnen gut verwenden, weil das Rechnen mit Logarithmen ein Rechnen mit Exponenten (bei gleicher Basis) ist. Damit wird das Multiplizieren bzw. das Dividieren auf das Addieren bzw. das Subtrahieren zurückgeführt. Auch das Potenzieren bzw. Radizieren wird auf das Multipliziern bzw. Dividieren zurückgeführt.

Zum logarithmischen Rechnen benötigt man die Logarithmen der Zahlen, mit denen gerechnet werden soll. Als praktisch haben sich dabei die Logarithmen zur Basis 10, die dekadischen Logarithmen erwiesen. Hierfür gilt folgende vereinfachte Schreibweise: ${\log }_{10}$b = lg b

Da $\lg \left(a\cdot {10}^n\right)=\lg a+\lg {10}^n=n+\lg a$ ist, genügt es, die dekadischen Logarithmen der Zahlen zwischen 1 und 10 zu kennen.
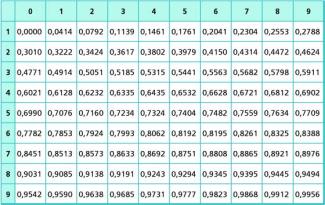
In der nebenstehenden Tabelle sind die Logarithmen der Zahlen von 1,0 bis 9,9 angeben.

Beispiele
Der Logarithmus von 2,5 ist also 0,3979.
Der von 25 ist dann 1,3979, weil $\lg 25=\lg 10\cdot \lg \mathrm{2,5}$
Analog ist lg 0,25 = 0,3979 - 1, weil lg 0,25 = lg (2,5 : 10) und damit lg 2,5 - lg ${10}^{-1}$ ist.

Die Ziffernfolge 3979 heißt Mantisse, die Zahl vor dem Komma oder die nachgestellte negative Zahl ist die Kennziffer. Ein Logarithmus besteht immer aus Kennziffer und Mantisse.
Will man nun z. B. $\mathrm{2,5}\cdot \mathrm{3,4}$ rechnen, so sucht man die Logarithmen beider Zahlen heraus. Sie lauten 0,3979 und 0,5315.
Addiert man diese, erhält man 0,9294. Diesem Logarithmus entspricht der Wert 8,5. Also ist $\mathrm{2,5}\cdot \mathrm{3,4}$= 8,5.

In analoger Weise lassen sich Divisionsaufgaben rechnen, man muss den Logarithmus des Divisors von dem des Dividenden subtrahieren.
Will man eine Potenz berechnen, muss man den Logarithmus der Basis mit dem Exponenten multiplizieren.
Will man eine Wurzel ziehen, ist der Logarithmus des Radikanden durch den Wurzelexponenten zu teilen.
In allen Fällen muss man dann natürlich zum erhaltenen Logarithmus aus der Tabelle den jeweils zugehörigen Wert ermitteln.

In der Vergangenheit, als es noch keine elektronischen Rechenhilfsmittel gab, hat das logarithmische Rechnen eine große Rolle gespielt. Aber auch in modernen Rechenhilfsmitteln werden z. T. noch die Eigenschaften der Logarithmen genutzt.

Der Begriff Logarithmus geht auf MICHAEL STIFEL (1487 bis 1567) zurück, der auch schon wesentliche Eigenschaften des Logarithmus entdeckte. Ausgangspunkt waren dabei Vergleiche von arithmetischen und geometrischen Reihen.

Mit dem Berechnen von Logarithmentafeln wurden die Logarithmen in der ersten Hälfte des 17. Jahrhunderts für die praktische Anwendung nutzbar gemacht.

Die erste Logarithmentafel gab 1614 JOHN NAPIER (1550 bis 1617) heraus.
1620 erschienen die Tafeln von JOST BÜRGI (1552 bis 1632) und 1617 die von HENRI BRIGGS (1561 bis 1630), der erstmals dekadische Logarithmen verwandte. Seine 1624 erschienene Arithmetica logarithmica enthielt die dekadischen Logarithmen der ganzen Zahlen von 1 bis 20000 und von 90000 bis 100000 auf 14 Stellen genau.
Die verbleibende Lücke wurde von dem Holländer EZECHIL DE DECKER geschlossen, der 1627 mit Unterstützung von ADRIAEN VLACQ (etwa 1600 bis 1677) eine vollständige Logarithmentafel veröffentlichte.
Mathematiker und Astronomen, so z. B. JOHANNES KEPLER (1571 bis 1630) begrüßten und benutzten die neue Entdeckung, die die oftmals aufwendigen Rechenarbeiten wesentlich vereinfachten.

Der Engländer EDMUND GUNTER (1581 bis 1626) erfand die logarithmische Teilung. Dabei werden ausgehend von 1 die Logarithmen der Zahlen als Längen abgetragen.