Simulation, Zufallsexperimente
Tabellenkalkulationen und Computeralgebrasysteme (CAS) eignen sich auch als Hilfsmittel zur Simulation realer Vorgänge. Mithilfe eines integrierten Zufallszahlengenarators ist es möglich, verschiedene Zufallsexperimente zu simulieren und mathematisch auszuwerten.
Tabellenkalkulationen und Computeralgebrasysteme (CAS) eignen sich auch als Hilfsmittel zur Simulation realer Vorgänge. Mithilfe eines integrierten Zufallszahlengenarators ist es möglich, verschiedene Zufallsexperimente zu simulieren und mathematisch auszuwerten.
| Simulation von Zufallsexperimenten mit Derive | Eingabe |
| Erzeugen einer ganzzahligen Zufallszahl aus dem Intervall 0 Z n mit n > 1 | RANDOM(n) |
| Werfen einer Münze mit 1 für Zahl und 0 für Wappen | RANDOM(2) |
| Werfen eines Würfels | 1 + RANDOM(6) |
| Ziehen einer Kugel aus einer Urne (Die Kugeln in der Urne sind von 1 bis n durchnummeriert.) | 1 + RANDOM(n) |
Beispiel:
Um nachzuweisen, dass die relative Häufigkeit für das Eintreten eines Ereignisses ein Maß für dessen Wahrscheinlichkeit ist, soll ein Würfel 1000-mal geworfen und das Auftreten einer „6“ registriert werden.
Anstelle die Random-Funktion 1000-mal nacheinander ausführen zu müssen, kann die Vektor-Funktion verwendet werden.
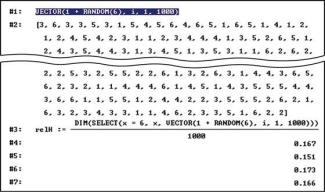
Der Befehl VECTOR(1+RANDOM(6),i,1,1000) stellt die 1000 Zufallszahlen als Liste dar (Bild 1). Nun kann die Anzahl der „gewürfelten“ Sechsen ermittelt und die relative Häufigkeit berechnet werden. Effektiver ist es aber, eine spezielle Funktion relH (relative Häufigkeiten) zu definieren, die das Eintreten einer „6“ bei 1 000 Würfen in einem Schritt ermittelt:
relH:=DIM(SELECT(x=6,x,VECTOR(1+RANDOM(6),i,1,1000)))/1000)
(Der SELECT-Befehl „sortiert“ die „gewürfelten“ Sechsen aus, der DIM-Befehl zählt sie.)
Das Ergebnis wird auch bei Wiederholung stets ein Wert um 0,17 sein. Die so ermittelte relative Häufigkeit stimmt näherungsweise mit der Wahrscheinlichkeit für das Eintreten einer „6“ überein, denn nach der LAPLACE-Regel gilt:
Eingaben zur Simulation von Zufallsexperimenten mit Exel
Erzeugen einer Zufallszahl aus dem Intervall 0 Z < 1:
= Zufallszahl ()
Erzeugen einer Zufallszahl aus dem Intervall 0 Z < m:
= m · Zufallszahl ()
Erzeugen einer Zufallszahl aus dem Intervall 1 Z < m:
= m · Zufallszahl () + 1
Erzeugen einer ganzzahligen Zufallszahl aus dem Intervall 1 Z < m
(Ziehen einer von m durchnummerierten Kugeln aus einer Urne):
= GANZZAHL(m · ZUFALLSZAHL() + 1)
Erzeugen einer Zufallszahl aus einer Zweiermenge {0; 1}
(Werfen einer Münze):
= GANZZAHL(2 · ZUFALLSZAHL())
Erzeugen einer Zufallszahl aus der Sechsermenge {1; 2; 3; 4, 5; 6}
(Werfen eines Würfels):
= GANZZAHL(6 · ZUFALLSZAHL() + 1)
-
1 000 Würfe mit der VECTOR-Funktion
keine Angabe
Beispiel: Gesetz der großen Zahlen
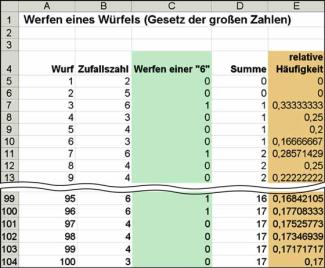
Auch mit einer Tabellenkalkulation kann eindrucksvoll nachgewiesen werden, dass die relative Häufigkeit für das Eintreten eines Ereignisses bei einer großen Anzahl von Versuchen stabil wird (Bild 2).
Untersucht wird das Auftreten einer „6“ bei 100 Würfen (Spalte A) mit einem regulären Würfel.
In Spalte B werden ganzzahlige Zufallszahlen der Menge {1; 2; 3; 4; 5; 6} erzeugt, in Spalte C wird mithilfe einer „WENN-Funktion“ registriert, ob eine „6“ gewürfelt wurde, in Spalte D wird die Anzahl der gewürfelten Sechsen fortlaufend addiert und in Spalte E werden die relativen Häufigkeiten für das Auftreten einer „6“ berechnet.
-
Gesetz der großen Zahlen
Die Zellenverknüpfungen sind folgendermaßen vorzunehmen:
Zelle B5: =GANZZAHL(6 * ZUFALLSZAHL() + 1)
Zelle C5: =WENN(B5 = 6; 1; 0)
Zelle D5: =C5
Zelle D6: =D5 + C6
Zelle E5: =D5/A5
Spalte E und vor allem die grafische Darstellung der relativen Häufigkeiten von Spalte E zeigen sehr anschaulich, dass sich für eine große Anzahl von Würfen ein Wert von annähernd 0,17 einstellt (Bild 3).
Mit Taste F9 kann die Versuchsreihe beliebig oft wiederholt werden. Zwar zeigt das Diagramm stets einen anderen Verlauf, letztlich aber stellt sich immer eine relative Häufigkeit um 0,17 ein.
-
Grafische Darstellung der relativen Häufigkeit

keine Angabe
Beispiel:
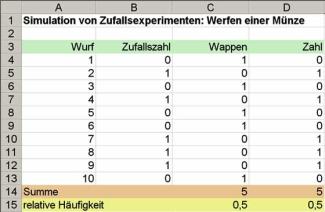
Mithilfe einer Tabellenkalkulation soll ein 10-maliger Münzwurf simuliert werden. Dabei ist die relative Häufigkeit für das Auftreten von „Wappen“ und „Zahl“ zu ermitteln.
Das Werfen einer Münze kann mithilfe der Zufallszahlen 0 und 1 simuliert werden, 0 stehe für „Wappen“ und 1 für „Zahl“.
Die anzulegende Kalkulationstabelle besteht aus vier Spalten. In Spalte A werden die Würfe fortlaufend nummeriert und in Spalte B die Zufallszahlen der Menge {0; 1} erzeugt.
Dazu wird in den Zellen B4 bis B13 eingetragen: =GANZZAHL(2*ZUFALLSZAHL()).
In den Spalten C und D wird registriert, ob „Wappen“ oder „Zahl“ geworfen wurde. Hier bedeutet eine eingetragene 1 „geworfen“ und eine eingetragene 0 „nicht geworfen“.
Erzeugt werden diese Eintragungen in den Spalten C und D mithilfe einer sogenannten WENN-Funktion:
WENN(B4 = 0; 1; 0) bedeutet, wenn in Zelle B4 die Zufallszahl 0 erscheint, wird eine 1 angezeigt, ansonsten eine 0 (Bild 4).
Die Eintragung erfolgt in Zelle C4: =WENN(B4 = 0; 1; 0) und wird dann auf C5 bis C13 kopiert.
Analog wird in Zelle D4: =WENN(B4 = 1; 1; 0) eingetragen und auf D5 bis D13 kopiert.
In den Zellen C14 und D14 wird gezählt, wie oft „Wappen“ und „Zahl“ geworfen wurden, in den Zellen C15 und D15 erfolgt die Berechnung der relativen Häufigkeiten.
Verwendet werden hierfür die Funktionen SUMME bzw. MITTELWERT:
Zelle C14: =SUMME(C4:C13);
Zelle D14: =SUMME(D4:D13);
Zelle C15: =MITTELWERT(C4:C13);
Zelle D15: =MITTELWERT(D4:D13)
Ist diese Kalkulationstabelle einmal angelegt, können mit der Taste F9 jederzeit zehn neue Würfe simuliert und ausgewertet werden.
-
10 Münzwürfe mit Tabellenkalkulation
Beispiel:
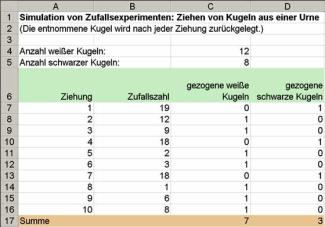
Ein häufig verwendetes Zufallsexperiment ist das Ziehen von Kugeln aus einer Urne.
Aus einer Urne mit zwölf weißen und acht schwarzen Kugeln sollen einzeln zehn Kugeln entnommen und sofort wieder zurückgelegt werden.
In Spalte A werden die Ziehungen fortlaufend gezählt und in Spalte B werden ganzzahlige Zufallszahlen der Menge {1; 20} erzeugt.
In den Spalten C und D wird erfasst, ob eine weiße bzw. eine schwarze Kugel gezogen wurde (Bild 5).
Dazu müssen folgende Zellenverknüpfungen vorgenommen werden:
Zelle B7: =GANZZAHL(($C$4 + $C$5) * ZUFALLSZAHL() + 1), dann auf B8 bis B16 kopieren
Zelle C7: =WENN(B7 <= $C$4; 1; 0), dann auf C8 bis C16 kopieren
Zelle D7: =WENN(B7 > $C$4; 1; 0), dann auf D8 bis D16 kopieren