Toleranzen, Rechnen

In vielen praktischen Anwendungen wird mit Zahlenwerten gemessener Größen gerechnet. Um die Güte eines angegebenen Maßes (Nennwert) abschätzen zu können, wird vor allem in technischen Bereichen zusätzlich ein Intervall angegeben, in welchem der wahre Wert der zu messenden Größe mit Sicherheit liegt. Das Intervall beschreibt also eine Abweichung, die bei der Messung zugelassen wird. Eine solche zulässige Abweichung vom wahren Wert einer gemessenen Größe heißt Toleranz. Den kleinsten Wert dieses Intervalls nennt man auch untere Wertschranke, den größten Wert obere Wertschranke. Für Wirtschaft und Industrie sind die zulässigen Toleranzen für viele Zwecke in DIN-Vorschriften geregelt.

Beispiel:
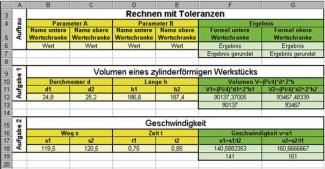
Die Angabe m = 500 g ± 20 g oder auch (500 ± 20) g auf einer Verpackung bedeutet, dass der wirkliche Wert der Masse m des betreffenden Inhaltes im Intervall 480 g $\le \text{m}\le$ 520 g liegt. Die untere Wertschranke beträgt also 480 g, die obere Wertschranke 520 g und die Toleranz 520 g – 480 g = 40 g.

Stellt man den Messwert mit der zugehörigen Toleranz auf einer Zahlengeraden dar, so erhält man eine Strecke, auf der der wahre Wert liegt (Bild 1).

Beispiel:
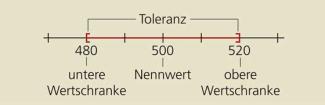
Die technische Zeichnung (Bild 2) zeigt ein Werkstück mit einer Bohrung. Die Tiefe der Bohrung ist ohne Toleranz, der Durchmesser der Bohrung ist mit Toleranz angegeben. Die Angabe $\cancel{○}{15}_0^{+\mathrm{0,2}}$ bedeutet, dass die Abweichung „nach unten“ 0 mm und „nach oben“ 0,2 mm betragen darf. Die untere Wertschranke beträgt 15 mm; die obere Wertschranke 15,2 mm. Der Durchmesser muss demnach im Intervall 15 mm $\le \text{d}\le$15,2 mm liegen.

Ist die Abweichung eines Messwertes vom wahren Wert nicht bekannt, so geht man in der Regel davon aus, dass die Abweichung des Näherungswertes vom wahren Wert maximal
0,5 Einheiten des Stellenwertes der letzten angegebenen Ziffer beträgt. Mit dieser Vereinbarung lassen sich nun wieder Wertschranken und ein gültiges Intervall für den wahren Wert angeben.

Beispiel:
Näherungswert: m = 500 g; d = 42,6 mm; v = 8,12 $\frac{\text{m}}{\text{s}}$
Stellenwert der letzten angegebenen Ziffer: Einer; Zehntel; Hundertstel
zulässige Abweichung: 0,5 g; 0,05 mm; 0,005$\frac{\text{m}}{\text{s}}$
untere Wertschranke: 499,5 g; 42,55 mm; 8,115$\frac{\text{m}}{\text{s}}$
obere Wertschranke: 500,5 g; 42,65 mm; 8,125$\frac{\text{m}}{\text{s}}$
Intervall für den wahren Wert: 499,5 g $\le \text{m}\le$ 500,5 g;
42,55 mm $\le \text{d}\le$ 42,65 mm; 8,115$\frac{\text{m}}{\text{s}}$ $\le \text{v}\le$8,125$\frac{\text{m}}{\text{s}}$

Gehen Näherungswerte in Rechnungen ein, kann auch das Ergebnis nur angenähert richtig sein. Das gilt auch für Zahlenwerte mit Toleranzangaben. Wird mit diesen Werten weitergerechnet, so beeinflussen die Toleranzen der Eingangswerte die Genauigkeit des Endergebnisses. Mithilfe der Wertschranken lässt sich diese Genauigkeit gut bestimmen. Da die Wertschranken nichts anderes als Intervallgrenzen sind, lassen sich die Regeln für das Rechnen mit Intervallen auch auf die Berechnung von Wertschranken anwenden. Die zum Teil aufwändigen Rechnungen können mithilfe eines Taschenrechners, aber auch mit einer Tabellenkalkulation ausgeführt werden.

Beispiele:
(1) Von einem zylinderförmigen Werkstück soll das Volumen berechnet werden.
Als Maße des Werkstücks gibt der Hersteller den Durchmesser mit d = (25,0 ± 0,2) mm und die Länge mit h = (187 ± 0,4) mm an. Für das Volumen gilt $\text{V = }\frac{\pi }{\text{4}}{\text{d}}^2\cdot \text{h}$.
Da die Näherungsgrößen d und h miteinander zu multiplizieren sind, werden für die untere Wertschranke des Volumens die unteren Wertschranken der Eingangsgrößen und für die obere Wertschranke des Volumens die oberen Wertschranken der Eingangsgrößen eingesetzt.
(2) In einem Experiment soll die Durchschnittsgeschwindigkeit eines sich bewegenden Körpers ermittelt werden.
Dazu werden der Weg s mit s = 120 cm und Zeit t mit t = 0,8 s gemessen und die Geschwindigkeit v nach der Formel $\text{v =}\frac{\text{s}}{\text{t}}$ berechnet.

Da im Beispiel (2) die Toleranzen der verwendeten Messgeräte nicht bekannt sind, ist hier von den Näherungswerten s = (120 ± 0,5) cm und t = (0,8 ± 0,05) s auszugehen. Nach der Regel für die Division von Intervallen erhält man die untere Wertschranke der Geschwindigkeit, indem die untere Wertschranke des Weges durch die obere Wertschranke der Zeit und die obere Wertschranke der Geschwindigkeit, indem die obere Wertschranke des Weges durch die untere Wertschranke der Zeit dividiert werden.
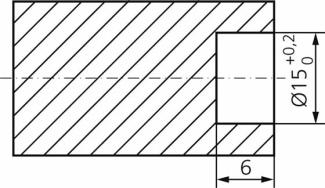
Für die Berechnungen empfehlen sich wieder Kalkulationstabellen. Gegenüber Berechnungen mit Taschenrechnern hat das den Vorteil, dass diese Tabellen für gleichartige Aufgaben immer wieder zur Verfügung stehen. Werden die Eingangswerte verändert, liefert die Kalkulationstabelle sofort das neue Ergebnis (Bild 3).