Trigonometrische Gleichungen

Trigonometrische Gleichungen (oder goniometrische Gleichungen genannt) sind solche Gleichungen, in denen die Unbekannte im Argument von Winkelfunktionen vorkommt.

Beispiele:
cos x = 0,5; sin x = 0,702;
tan x = 1,39; cos x + cos 2x = 1
In diesen Beispielen besteht die Aufgabe darin, den Winkel x im Gradmaß oder Bogenmaß zu bestimmen, der die Gleichung erfüllt.

Lösen von trigonometrischen Gleichungen bedeutet, Winkelgrößen zu bestimmen, welche die Gleichung erfüllen. Für einfache, in der Praxis jedoch durchaus häufig auftretende Fälle lassen sich durch geschicktes Umformen Lösungen finden. Oftmals muss man sich aber geeigneter Näherungsverfahren bedienen.

In den Fällen, in denen man einige Werte von Winkelfunktionen kennt, kann man eine Lösung sofort angeben.

Beispiel:
Da $\cos \text{ 60°}=\text{0}\text{,5}$ ist, kann man für cos x = 0,5 angeben, dass die Lösung
$x_1=60°$ ist.
Die Anzahl der Lösungen wird durch das vorgegebene Intervall bestimmt. Da die trigonometrischen Funktionen periodisch sind, findet man eine weitere Lösung im Intervall $\left[0;2\pi \right]$ mit $\cos \text{ x}=\text{cos }\left(\text{360°–}\text{x}\right)$,
d. h. $x_2=300°$.

Sind alle Lösungen (unabhängig von einem bestimmten Intervall) verlangt, dann gilt wegen der Periodizität
$x_1=\frac{\pi }{3}+2k\pi {\text{ und x}}_{\text{2}}=\frac{5\pi }{3}+2k\pi$ ,
wobei k eine beliebige ganze Zahl ist.

Außerdem ist noch zu beachten, ob die Lösungsangaben im Gradmaß oder Bogenmaß angegeben werden soll.
Ist Bogenmaß gefordert, so heißen die Lösungen aus dem Intervall $\left[0;2\pi \right]$:
$\begin{array}{l}{x}_1=60°{\text{ entspricht x}}_{\text{1}}=\frac{\pi }{3}\text{ und}\\ {\text{x}}_{\text{2}}=300°{\text{ entspricht x}}_{\text{2}}=\frac{5\pi }{3}\end{array}$

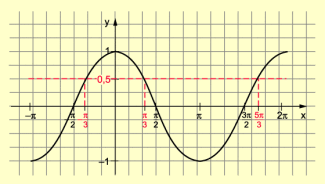
Die Lösungsmenge wird verständlich, wenn man den Graph der Kosinusfunktion und eine Parallele zur x-Achse im Abstand 0,5 zeichnet.
Die Abszissenwerte der Schnittstellen dieser Parallelen mit der Kosinuskurve liefern für unsere Beispielgleichung gerade die x-Werte, welche die Gleichung erfüllen.