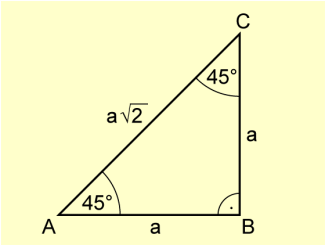
Winkelfunktionen am rechtwinkligen Dreieck
Bei allen zueinander ähnlichen rechtwinkligen Dreiecken sind die Quotienten aus den Längen von je zwei einander entsprechenden Seiten gleich.
Für die nebenstehend bzw. in Bild 1 dargestellten Dreiecke , die einander ähnlich sind, gilt nach den Ähnlichkeitssätzen:
Solche für zueinander ähnliche rechtwinklige Dreiecke übereinstimmenden Quotienten (Verhältnisse) werden mit Bezug auf einen der beiden nicht rechten Winkel als der Sinus, der Kosinus, der Tangens bzw. der Kotangens dieses Winkels bezeichnet.
Bei allen zueinander ähnlichen rechtwinkligen Dreiecken sind die Quotienten aus den Längen von je zwei einander entsprechenden Seiten gleich.
Für die in nebenstehendem Bild 1 dargestellten Dreiecke, die zueinander ähnlich sind, gilt nach den Ähnlichkeitssätzen:
Solche für zueinander ähnliche rechtwinklige Dreiecke übereinstimmenden Quotienten (Verhältnisse) werden mit Bezug auf einen der beiden nicht rechten Winkel als der Sinus, der Kosinus, der Tangens bzw. der Kotangens dieses Winkels bezeichnet. Bezogen auf obiges Dreieck, für das die Seiten
die Ankatheten des Winkels ,
die Gegenkatheten des Winkels ,
Hypotenusen sind, heißt
der Sinus des Winkels (kurz: sin ),
der Kosinus des Winkels (kurz: cos ),
der Tangens des Winkels (kurz: tan ).
Der Kehrwert des Tangens eines Winkels heißt der Kotangens von (kurz: cot ).
Aus dem Bild 1 kann man zugleich entnehmen:
Der Sinus des Winkels ist gleich dem Kosinus des Winkels
der Kosinus des Winkels ist gleich dem Sinus des Winkels
der Tangens des Winkels ist gleich dem Kotangens des Winkels
der Kotangens des Winkels ist gleich dem Tangens des Winkels
Unter Verwendung spezieller rechtwinkliger Dreiecke lassen sich die Sinus-, Kosinus-, Tangens- und Kotangenswerte einiger Winkel berechnen.
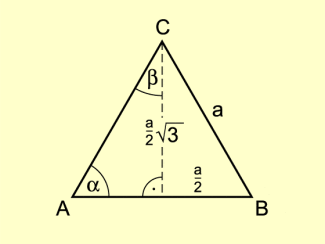
Für jedes durch eine Höhe in zwei zueinander kongruente rechtwinklige Dreiecke geteiltes gleichseitiges Dreieck ABC gilt:
-
Zueinander ähnliche rechtwinklige Dreiecke
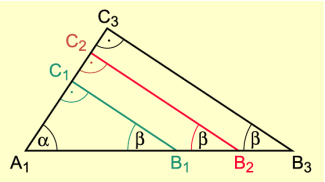
Daraus folgt (Bild 2):
-
Gleichseitiges Dreieck
An einem gleichschenklig-rechtwinkligen Dreieck mit kann man ablesen (Bild 3):
-
Gleichschenklig-rechtwinkliges Dreieck