Winkelfunktionswerte, Beziehungen

Zwischen Funktionswerten der verschiedenen Winkelfunktionen bestehen vielfältige Beziehungen, deren Kenntnis für die Untersuchung theoretischer Zusammenhänge wie auch für Berechnungen sehr vorteilhaft sein können. Dies betrifft sowohl die Funktionswerte verschiedener Winkelfunktionen zu ein und demselben Argument als auch die Werte einer bestimmten Winkelfunktion für verschiedene Argumente.

Zusammenhang zwischen den Sinus- und Kosinusfunktionswerten desselben Winkels

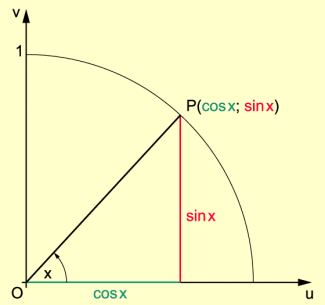
Die Figur im Bild 1 zeigt einen Vierteleinheitskreis. Das Dreieck ${\text{OQP}}_{\text{1}}$ ist rechtwinklig und somit folgt:
$\text{sin}{}^{\text{2}}\text{x}+\text{cos}{}^{\text{2}}\text{x}=\text{1}$
Diese Beziehung gilt für alle Winkel x $\left(x\ne k\cdot \frac{\pi }{2},k\in \mathbb{Z}\right)$ und trifft wegen ${\text{0}}^{\text{2}}+{\text{1}}^{\text{2}}={\text{1}}^{\text{2}}+{\text{0}}^{\text{2}}=\text{1}$ sogar auf Winkel $x=k\cdot \frac{\pi }{2}$ zu, obwohl dann das o.g. rechtwinklige Dreieck nicht mehr existiert.

Unter Verwendung der angegebenen Formel sowie der Beziehung $\text{tan}\text{x}=\frac{\text{sin}\text{x}}{\text{cos}\text{x}}$ kann man aus dem Funktionswert eines Arguments für eine der drei Winkelfunktionen auch unmittelbar (d. h., ohne vorher den entsprechenden Winkel zu bestimmen) die Werte für die anderen beiden berechnen bzw. entsprechende Formeln aufstellen.

Beispiel:
Gegeben: sin x = 0,6
Gesucht: cos x, tanx
$\begin{array}{l}{\text{cos}}^{\text{2}}\text{x}=\text{1}-{\text{sin}}^{\text{2}}\text{x}\text{,}\text{also}\text{cos}\text{x}=\sqrt{1-{\mathrm{0,6}}^2}=\sqrt{\mathrm{0,64}}=\text{0}\text{,8}\\ \text{tan}\text{x}=\frac{\text{0}\text{,6}}{\text{0}\text{,8}}=\text{0}\text{,75}\end{array}$
Diese Berechnung bezieht sich auf Winkel aus dem I. Quadranten.
Ohne diese Beschränkung müsste auch cos x = –0,8 und damit zusätzlich tan x = –0,75 einbezogen werden.

Allgemein ergeben sich aus $\text{sin}{}^{\text{2}}\text{x}+\text{cos}{}^{\text{2}}\text{x}=\text{1}$ und $\text{tan}\text{x}=\frac{\text{sin}\text{x}}{\text{cos}\text{x}}$ folgende Umrechnungsformeln (bezogen auf Winkel aus dem
I. Quadranten):