Winkelhalbierende im Dreieck

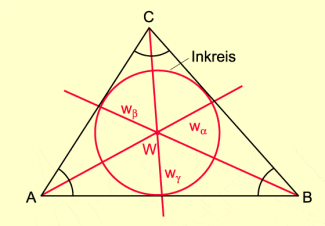
Die Winkelhalbierenden halbieren die drei Innenwinkel des Dreiecks. Die drei Winkelhalbierenden schneiden einander in genau einem Punkt. Dieser Punkt ist Mittelpunkt des Kreises, der die drei Dreiecksseiten von innen berührt. Man nennt deshalb diesen Kreis den Inkreis des Dreiecks.

Winkelhalbierende und Inkreis

#Winkelhalbierende #Inkreis #Inkreismittelpunkt #Lot

Die Winkelhalbierenden halbieren die drei Innenwinkel des Dreiecks. Die drei Winkelhalbierenden schneiden einander in genau einem Punkt. Dieser Punkt ist Mittelpunkt des Kreises, der die drei Dreiecksseiten von innen berührt. Man nennt deshalb diesen Kreis den Inkreis des Dreiecks (Bild 1).

Winkelhalbierende der Innenwinkel des Dreiecks

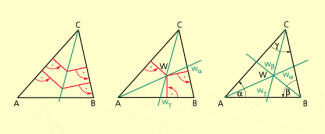
Beweis (Bild 2):

Jeder Punkt einer Winkelhalbierenden hat von den Schenkeln des Winkels denselben Abstand (sww).
In einem Dreieck ABC ist der Schnittpunkt W von $w_{α}$ und $w_{γ}$ einerseits von den Seiten $\bar{A C}$ und $\bar{A B}$ ,
andererseits von $\bar{B C}$ und $\bar{A C}$ gleich weit entfernt.
Also hat W von allen drei Seiten denselben Abstand, insbesondere auch von $\bar{B C}$ und $\bar{A B}$ .
W muss demnach auch auf $w_{β}$ liegen. (w. z. b. w.)

Der Inkreismittelpunkt liegt bei allen Dreiecken innerhalb der Figur.

Beweisfiguren

Material zum Thema

wh_inkr.pdf

wh_inkr.pdf

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Winkelhalbierende im Dreieck

Winkelhalbierende und Inkreis

wh_inkr.pdf

Rechtliches

Einloggen