- Lexikon
- Physik Abitur
- 2 Mechanik
- 2.7 Gravitation
- 2.7.3 Körper in Gravitationsfeldern
- Bahnformen und Energie von Satelliten
Bahnformen und Energie von Satelliten
Erdnahe Bahnen
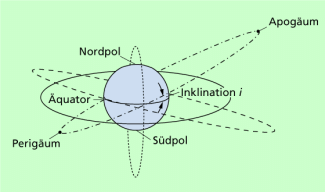
Die meisten künstlichen Satelliten bewegen sich auf elliptischen Bahnen um die Erde, wobei sie den keplerschen Gesetzen folgen. In Bild 1 sind die wichtigsten Bahnparameter angegeben. Das Perigäum ist der erdnächste Punkt einer Satellitenbahn. Der Flugkörper besitzt hier seine größte Geschwindigkeit. Das Apogäum ist der erdfernste Punkt. Der Satellit bewegt sich in der Nähe dieses Punktes am langsamsten.
Die Bahnneigung oder Inklination ist der in Gradmaß angegebene Winkel zwischen der Ebene der Satellitenbahn und der Ebene des Erdäquators. Beträgt die Inklination 90°, so verläuft die Bahn über die Pole und wird als Polarbahn bezeichnet. Ist die Bahnneigung 0°, so befindet sich der Flugkörper auf einer Bahn über dem Äquator (äquatoriale Bahn).
Ohne größere Bahnkorrekturen kann man einen Satelliten nur von einem äquatornahen Startplatz in eine Umlaufbahn mit der Inklination 0° bringen. Ein solcher Startplatz am Äquator hat zusätzlich den Vorteil, dass beim Start in Richtung Erddrehung (nach Osten) ein merklichen Teil der notwendigen Bahngeschwindigkeit durch die Eigendrehung der Erde, also quasi umsonst, zur Verfügung steht. Weiter nördlich oder südlich gelegene Startrampen befinden sich näher an der Erdachse. Entsprechend größer ist der Energiebedarf beim Start.
Damit ein Satellit eine erdnahe Bahn erreicht, ist eine Geschwindigkeit zwischen 7,9 km/s (1. kosmische Geschwindigkeit, minimale Kreisbahngeschwindigkeit) und 11,2 km/s (2. kosmische Geschwindigkeit, Fluchtgeschwindigkeit) erforderlich. Die Bahn ist in der Regel davon abhängig, für welchen Zweck der Satellit genutzt werden soll.
Geostationäre Bahnen
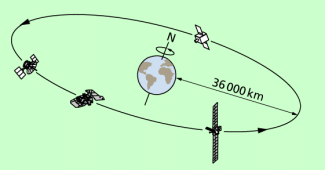
Als geostationär bezeichnet man die Bahn eines Raumflugkörpers, der sich ständig mit der gleichen Winkelgeschwindigkeit bewegt, mit der die Erde um ihre Achse rotiert. Der Radius der Flugbahn beträgt etwa 42.000 km. Der Satellit steht dabei über einem Punkt des Äquators. Man kann den Bahnradius relativ einfach berechnen, wenn man davon ausgeht, dass die Radialkraft (Zentralkraft), die den Satelliten auf seiner Bahn hält, gleich der Gravitationskraft zwischen Erde und Satellit ist:
Ein solcher geostationärer Satellit bewegt sich auf einer Bahn mit einem Radius von 42230 km. Das ist eine Höhe von
42230 km - 6371 km = 35859 km oder von rund 36000 km über der Erdoberfläche.
HOHMANN-Bahnen
Der deutsche Ingenieur WALTER HOHMANN (1880-1945) beschäftigte sich mit Problemen der Raumfahrt. In seinem 1925 veröffentlichten Buch „Die Erreichbarkeit der Himmelskörper“ beschrieb er mögliche Flugbahnen interplanetarer Raumfahrzeuge, die man heute als HOHMANN-Bahnen bezeichnet.
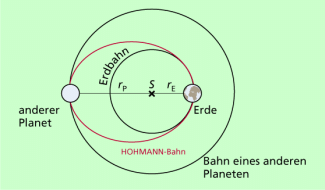
Die Grundidee ist dabei, solche Flugbahnen zu finden, bei denen ein Raumflugkörper möglichst ohne Verbrauch von Treibstoff sein Ziel erreicht. Nach HOHMANN besteht eine Möglichkeit darin, die Flugbahn so zu wählen, dass der Raumflugkörper eine elliptische Bahn hat, die die Erdbahn und die Bahn des Zielplaneten tangential berührt (Bild 3). Solche HOHMANN-Bahnen sind vor allem eine energiesparende Variante einer Flugbahn und insofern bedeutsam für die Realisierung interplanetarer Flüge.
Swing-by-Technik
Einen besonderen Typ von Flugbahnen erhält man durch Nutzung der Gravitationsfelder und der Eigenbewegung anderer Planeten. Man spricht dann von der Swing-by-Technik. Das Prinzip besteht in folgendem: Nähert sich eine Raumsonde einem anderen Planeten, so wird sie im Gravitationsfeld dieses Planeten beschleunigt. Darüber hinaus wird die Bahnform der Sonde beeinflusst. Es lässt sich auf diese Weise ohne irgendeinen Antrieb die Bahngeschwindigkeit und die Flugbahn einer Raumsonde ändern. Nach dem Energieerhaltungssatz muss die zusätzliche kinetische Energie, die eine Sonde erhält, vom betreffenden Himmelskörper stammen. Angesichts der Masseverhältnisse ist dessen Geschwindigkeitsverringerung vernachlässigbar klein.
Genutzt wurde die Swing-by-Technik beispielsweise bei den amerikanischen Voyager-Sonden. Die 1977 gestarteten Sonden Voyager 1 und Voyager 2 führten 1979 an Jupiter ein Swing-by-Manöver durch. Dadurch wurde erreicht, dass die Sonden 1980/81 den Saturn anflogen und zahlreiche Aufnahmen von diesem Planeten machten. Voyager 2 wurde in Richtung Uranus und später in Richtung Pluto umgelenkt und lieferte die ersten Fotos von diesen Planeten. Beide Sonden sind nicht mehr aktiv. Es dürften die ersten Sonden sein, die die Grenze unseres Sonnensystems erreichen.
Bemerkungen zur Energie von künstlichen Satelliten und Sonden
Für Satelliten auf einer Erdumlaufbahn gilt, dass sie zum einen auf eine bestimmte Bahn über der Erdoberfläche transportiert werden müssen. Dazu ist Arbeit im Gravitationsfeld der Erde erforderlich. Die Satelliten besitzen damit bezüglich der Erdoberfläche eine bestimmte potenzielle Energie, die ihrer Höhe über der Erdoberfläche abhängt. Für den Transport in eine bestimmte Höhe und damit für ihre potenzielle Energie in dieser Höhe gilt:
Darüber hinaus muss sich der Satellit längs seiner Bahn mit einer bestimmten Bahngeschwindigkeit bewegen, ansonsten würde er in Richtung Erde stürzen
Damit besitzt er eine bestimmte kinetische Energie:
Kinetische und potenzielle Energie liegen bei Satelliten in einer Erdumlaufbahn meist in der gleichen Größenordnung.
Beispiel: Für einen Satelliten mit einer Masse von 1000 kg ergeben sich bei einer kreisförmigen Bahn folgende Werte:
| Höhe über der Erdoberfläche | potenzielle Energie | kinetische Energie |
| 500 km | ||
| 36 000 km |
Die Gesamtenergie ergibt sich als Summe von potenzieller und kinetischer Energie.
Bei Raumsonden, die den Bereich der Erde verlassen, spielen potenzielle und kinetische Energie eine unterschiedliche Rolle. Eine bestimmte Geschwindigkeit und damit eine bestimmte kinetische Energie ist Voraussetzung dafür, dass der Bereich der Erde überhaupt verlassen werden kann. Diese Geschwindigkeit ist die 2. kosmische Geschwindigkeit (Fluchtgeschwindigkeit), die für die Erde einen Wert von 11,2 km/s hat.
Die potenzielle Energie einer Raumsonde hängt dann entscheidend davon ab, wo sie sich befindet. Sie spielt insofern eine Rolle, als Geschwindigkeit und Bahnform durch Gravitationsfelder beeinflusst werden können und sich mit der Bewegung auch die potenzielle Energie der Sonde ständig ändert. Trotzdem gilt auch für Raumsonden der Energieerhaltungssatz. Es muss dabei aber beachtet werden, dass zu dem betreffenden abgeschlossenen System alle Körper mit ihren Gravitationsfeldern gehören, mit denen die Sonde in Wechselwirkung tritt.
polare Bahn Berechnung äquatoriale Bahn potenzielle Energie Inklination Apogäum Swing-by-Manöver Perigäum Hohmann-Bahnen Voyager-Sonden Äquatorbahn keplersche Gesetze Energie von Satelliten Zentralkraft Polarbahn Erdäquator Energieerhaltungssatz Satellitenbahn Gravitationskraft Bahnneigung Bahnformen Fluchtgeschwindigkeit kinetische Energie geostationäre Bahn Radialkraft Walter Hohmann potentielle Energie Erdumlaufbahn Rechenbeispiel Swing-by-Technik
Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.
Ein Angebot von 