Gravitation und Gravitationsgesetz
Alle Körper ziehen sich aufgrund ihrer Massen gegenseitig an. So zieht z. B. die Erde den Mond an. Umgekehrt zieht auch der Mond die Erde an.
Die gegenseitige Anziehung von Körpern aufgrund ihrer Massen wird Massenanziehung oder Gravitation (gravis, lat.: schwer) genannt. Die dabei wirkenden Kräfte werden als Schwerkräfte oder als Gravitationskräfte bezeichnet.
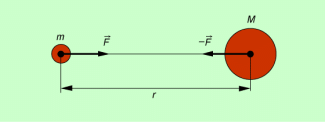
Die Gravitationskraft zwischen zwei Körpern kann mit dem Gravitationsgesetz berechnet werden. Sie ist umso größer,
- je größer die Massen der Körper sind und
- je kleiner der Abstand ihrer Massenmittelpunkte voneinander ist.
Gravitation und Gravitationsgesetz
Alle Körper ziehen sich aufgrund ihrer Massen gegenseitig an. So zieht z. B. die Erde den Mond an. Umgekehrt zieht auch der Mond die Erde an.
Die gegenseitige Anziehung von Körpern aufgrund ihrer Massen wird Massenanziehung oder Gravitation (gravis, lat.: schwer) genannt. Die dabei wirkenden Kräfte werden als Schwerkräfte oder als Gravitationskräfte bezeichnet.
Das Gravitationsgesetz
Die Gravitationskraft zwischen zwei Körpern kann mithilfe des Gravitationsgesetz es gerechnet werden. Dieses Gesetz wurde von dem englischen Naturforscher ISAAC NEWTON (1643-1727) um das Jahr 1687 herum entdeckt.
Die Historie dieses Gesetzes ist von Legenden umgeben. So soll ISAAC NEWTON an einem schönen Sommertag unter einem Apfelbaum gelegen haben und von einem herabfallenden Apfel getroffen worden sein. Das habe ihn zu der Überlegung angeregt, was die Ursache dafür ist, dass ein Apfel in Richtung Erdoberfläche fällt.
Belegt ist, dass sich im 17. Jahrhundert verschiedene Gelehrte, z.B. auch der Astronom EDMOND HALLEY (1656-1743), mit dem Zusammenhang zwischen der Kraft zwischen zwei Körpern und ihrem Abstand beschäftigten. Mithilfe der sogenannten Mondrechnung konnte NEWTON zeigen, dass es sich bei der zwischen Himmelskörpern wirkenden Kraft um die gleiche Art von Kraft handelt, die auch Körper in Richtung Erdoberfläche beschleunigt.
NEWTON ging bei seinen Überlegungen von einer näherungsweisen Kreisbewegung des Mondes um die Erde aus. Die in Richtung Erde wirkende Radialbeschleunigung beträgt dann nach den Gesetzen der Kreisbewegung:
Dabei sind T die siderische Umlaufzeit des Mondes um die Erde (27,32 d) und r der mittlere Mondbahnradius (384 400 km). NEWTON wusste darüber hinaus: Der Radius r der Mondbahn um die Erde ist etwa 60-mal größer als der Erdradius R. Für das Verhältnis der Radialbeschleunigung a des Mondes und der Fallbeschleunigung g an der Erdoberfläche gilt näherungsweise:
Sind beide Beschleunigungen auf dieselbe Kraft zurückzuführen, dann müsste für diese Kraft eine Entfernungsabhängigkeit in der Form
gelten. Diesen Zusammenhang fand NEWTON bereits um 1665, die Formulierung des Gravitationsgesetzes erst ca. 20 Jahre später.
Das Gravitationsgesetz lautet in der heute üblichen Formulierung:
Die zwischen zwei Körpern wirkende Gravitationskraft kann mit folgender Gleichung berechnet werden:
Beispiele für Gravitationskräfte und ihr Wirken
Bekannt sind vor allem die Gravitationskräfte zwischen der Erde und auf ihr befindlichen Körpern. Diese Erdanziehungskraft bewirkt, dass ein Apfel, wenn man ihn loslässt, senkrecht nach unten fällt. Ein Schrank drückt auf seine Unterlage, den Boden. Ein Kind, das auf einer Schaukel sitzt, zieht an der Aufhängung der Schaukel.
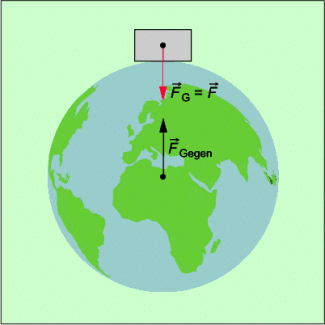
Die Erdanziehungskraft wird häufig auch als Gewichtskraft bezeichnet. Die Gewichtskraft ist die Gravitationskraft, mit der ein Körper von der Erde angezogen wird (Bild 2).
Jeder Körper auf der Erdoberfläche oder in der Nähe der Erde von dieser angezogen. Zugleich zieht auch jeder Körper die Erde an. Diese Kraft (Bild 3) ist nach dem Wechselwirkungsgesetz der Gewichtskraft entgegen gerichtet und hat den gleichen Betrag. Wenn also z. B. die Gewichtskraft einer Person 620 N beträgt, dann wird sie mit einer Kraft von 620 N von der Erde angezogen. Zugleich zieht sie die Erde mit genau dieser Kraft an.
Gravitationskräfte wirken nicht nur zwischen der Erde und dem Mond oder zwischen der Erde und auf ihr befindlichen Körpern. Gravitation tritt vielmehr zwischen beliebigen Körpern auf, die eine Masse besitzen. Häufig sind aber die dabei auftretenden Gravitationskräfte so klein, dass man sie vernachlässigen kann. So beträgt z. B. die Gravitationskraft zwischen zwei Personen, die je eine Masse von 50 kg haben und die sich in einem Abstand von 1 m voneinander befinden, etwa F = 0,000.000.007 N.
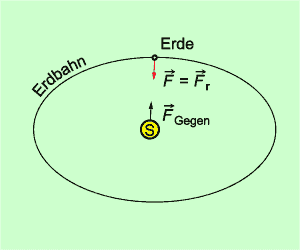
Gravitationskräfte bestimmen auch die Bewegung von Himmelskörpern sowie von künstlichen Satelliten und Raumstationen. So bewegt sich z. B. die Erde auf einer näherungsweise kreisförmigen Bahn um die Sonne (Bild 4). Der Mond oder künstliche Satelliten bewegen sich um die Erde. Damit sich aber ein Körper auf einer kreisförmigen Bahn bewegt, muss eine Kraft in Richtung des Zentrums der Bewegung wirken (Radialkraft oder Zentralkraft). Diese Kraft ist die Gravitationskraft, die die Sonne bzw. die Erde auf die Körper ausübt, die sich um sie bewegen.