Feldstärke und dielektrische Verschiebung

Elektrische Felder können mithilfe von Feldlinienbildern beschrieben werden. Zur ihrer quantitativen Beschreibung nutzt man die feldbeschreibenden Größen elektrische Feldstärke und dielektrische Verschiebung. Die elektrische Feldstärke E ist definiert als Quotient aus der Kraft F, die das Feld auf einen positiv geladenen Probekörper ausübt, und dessen Ladung Q:
$\vec{E} = \frac{\vec{F}}{Q}$
Die dielektrische Verschiebung D (Verschiebungsdichte) ist ein Maß für die auf einer Fläche im elektrischen Feld durch Influenz hervorgerufenen Ladung:
$D = \frac{Q}{A}$
Beide Größen sind durch die elektrische Feldkonstante und die Permittivitätszahl miteinander verbunden:
$\vec{D} = ε_{0} \cdot ε_{r} \cdot \vec{E}$
Bevorzugt wird mit der elektrischen Feldstärke gearbeitet.

Magnetisches Feld

#Magnet #magnetisches Feld #Feldlinien #Erdmagnetfeld #Magnetfeld der Erde

Magnete

#Magnet #Dauermagnet #Elementarmagnet #Magnetfeld

Elektrische Felder können in unterschiedlicher Weise beschrieben werden. Eine Möglichkeit ist ihre Beschreibung mithilfe von Feldlinienbildern. Genauere Hinweise dazu sind unter diesem Stichwort zu finden. Zur quantitativen Kennzeichnung eines elektrischen Feldes reicht aber ein Feldlinienbild nicht aus. Es sind physikalische Größen erforderlich.

Die elektrische Feldstärke

Zur genaueren Kennzeichnung eines elektrischen Feldes kann man den Betrag und die Richtung der Kraft auf einen Probekörper bestimmen, der sich in diesem Feld befindet. Die Kraft, die auf einen Körper bestimmter Ladung in einem Punkt des Feldes wirkt, ist ein Maß für die Stärke und die Richtung des Feldes in diesem Punkt. Die Größe wird als elektrische Feldstärke bezeichnet und ist folgendermaßen definiert:
Die elektrische Feldstärke E in einem Punkt gibt an, wie groß die Kraft auf eine positive Probeladung in diesem Punkt ist. Sie kann mit folgender Gleichung berechnet werden:
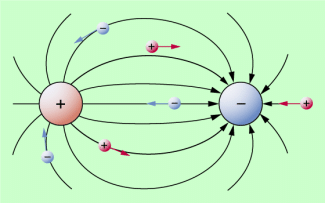
$\begin{array}{l} \vec{E} = \frac{\vec{F}}{Q} \\ F Kraft auf einen positiv geladenen Körper \\ Q Ladung dieses Körpers \end{array}$
Die Kraft F wird auch als Feldkraft bezeichnet. Die elektrische Feldstärke ist eine vektorielle Größe , deren Richtung mit der Kraftrichtung auf einen positiv geladenen Körper im Feld übereinstimmt (Bild 1). Trägt der Körper eine negative Ladung, so sind Kraftrichtung und Feldrichtung entgegengesetzt. Als Einheit der Feldstärke ergibt sich 1 N/C. Es gilt:
$\begin{array}{l} 1 \frac{N}{C} = 1 \frac{\frac{kg \cdot m}{s^{2}}}{A \cdot s} \\ Die Einheit 1 \frac{kg \cdot m}{s^{2}} im Zähler kann man mit \frac{m}{m} erweitern und \\ erhält 1 \frac{kg \cdot m^{2}}{s^{2} \cdot m} . \\ Nun ist 1 \frac{kg \cdot m^{2}}{s^{2}} = 1 N \cdot m = 1 W \cdot s = 1 V \cdot A \cdot s . \\ Damit erhält man: \\ 1 \frac{N}{C} = 1 \frac{V \cdot A \cdot s}{A \cdot s \cdot m} = 1 \frac{V}{m} \end{array}$

Die dielektrische Verschiebung

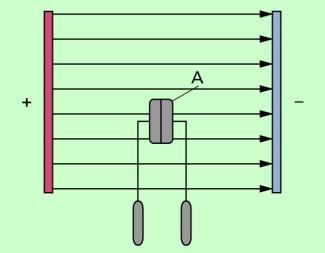
Bringt man, wie in Bild 2 dargestellt, zwei ungeladene metallische Blättchen, die eng aneinanderliegen und folglich leitend miteinander verbunden sind, in ein elektrisches Feld, so erfolgt bei den Blättchen Influenz (Ladungstrennung). Diese ist umso stärker, je stärker das elektrische Feld ist. Quantitativ kann man das erfassen, wenn man die Blättchen im Feld voneinander trennt und anschließend ihre Ladung bestimmt. Man erhält dann die Flächenladungsdichte :
$σ = \frac{Q}{A}$
Damit hat man eine skalare Größe zur Charakterisierung des Feldes. Zur Bestimmung der Richtung des Feldes kann die Flächennormale, also ein zur Fläche senkrecht stehender Vektor, genutzt werden. Das ist sinnvoll, weil elektrische Feldlinien senkrecht aus Leiterflächen austreten und damit stets die Richtung der Feldlinien mit der Richtung der Flächennormalen übereinstimmt. Die betreffende vektorielle Größe wird als dielektrische Verschiebung $\vec{D}$ oder auch als Verschiebungsdichte bezeichnet. Somit gilt:
Die dielektrische Verschiebung ist ein Maß für die auf einer Fläche im elektrischen Feld hervorgerufenen Ladung und damit zugleich auch ein Maß für die Stärke des elektrischen Feldes im betreffenden Bereich. Ihr Betrag ergibt sich als Quotient aus influenzierter Ladung Q und Fläche A, ihre Richtung ist gleich der Richtung der Flächennormalen.

Zusammenhang zwischen elektrischer Feldstärke und dielektrischer Verschiebung

Da sowohl durch die elektrische Feldstärke als auch durch die dielektrische Verschiebung ein und dasselbe elektrische Feld beschrieben werden kann, muss es zwischen beiden Größen einen Zusammenhang geben. Sie sind durch die elektrische Feldkonstante und die Permittivitätszahl (auch Dielektrizitätszahl und Dielektrizitätskonstante genannt) miteinander verknüpft. Es gilt:

$\begin{array}{l} \vec{D} = ε_{0} \cdot ε_{r} \cdot \vec{E} \\ ε_{0} elektrische Feldkonstante \\ ε_{r} Permittivitätszahl \\ (für Vakuum und Luft ist ε_{r} = 1, damit \\ vereinfacht sich die Gleichung zu \\ \vec{D} = ε_{0} \cdot \vec{E}) \end{array}$
Elektrische Feldstärke und dielektrische Verschiebung haben die gleiche Richtung, aber unterschiedliche Beträge und natürlich auch unterschiedliche Einheiten. Heute wird meist nur noch mit einer der beiden Feldgrößen gearbeitet und dabei die elektrische Feldstärke bevorzugt.

Elektrische Feldstärke in speziellen elektrischen Feldern

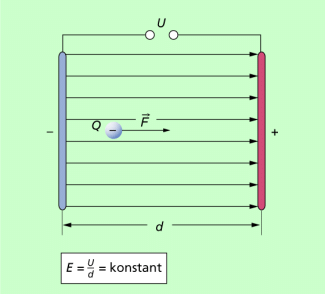
Ein homogenes Feld ist dadurch gekennzeichnet, dass die Feldlinien parallel verlaufen (Bild 3) und die elektrische Feldstärke an allen Stellen des Feldes gleich groß ist. Den Betrag der Feldstärke kann man durch folgende Überlegung ermitteln (Bild 3):
Für die Verschiebung einer Ladung Q im elektrischen Feld ist eine Arbeit erforderlich:
$\begin{array}{l} W = F \cdot d (1) \\ Sie ist gleich der elektrischen Arbeit \\ W = U \cdot I \cdot t und mit I \cdot t = Q \\ W = U \cdot Q (2) \\ Ein Gleichsetzen der rechten Seiten von (1) und (2) ergibt: \\ F \cdot d = U \cdot Q und nach Umformung: \\ \frac{F}{Q} = \frac{U}{d} \\ Der rechts stehende Quotient ist die \\ elektrische Feldstärke E, sodass man auch \\ schreiben kann: \\ E = \frac{U}{d} \end{array}$
Damit verfügt man über eine einfache Gleichung zur Berechung der Feldstärke im homogenen elektrischen Feld. Sie ist z.B. im Inneren eines Plattenkondensators nur von der Spannung zwischen den Platten und dem Plattenabstand abhängig.

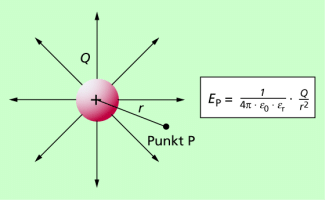
Relativ einfach berechnen lässt sich auch die elektrische Feldstärke in einem Radialfeld einer Punktladung (Bild 4), also für ein inhomogenes Feld. Für die Feldstärke in einem solchen Feld gilt:
$\begin{array}{l} E = \frac{1}{4 π \cdot ε_{0} \cdot ε_{r}} \cdot \frac{Q}{r^{2}} \\ ε_{0} elektrische Feldkonstante \\ ε_{r} Permittivitätszahl (Dielektrizitätszahl) \\ Q felderzeugende Ladung \\ r Abstand von der felderzeugenden Ladung \end{array}$
Die Feldstärke hängt somit von der Größe der felderzeugenden Ladung und davon ab, wie groß der Abstand von ihr ist, wobei sich der Betrag der Feldstärke mit dem Quadrat des Abstandes verringert.

Überlagerung elektrischer Felder

Wirken auf einen geladenen Körper mehrere elektrische Felder ein, dann gilt für die auf den Körper wirkende Kraft das Superpositionsprinzip:
Beim Wirken mehrere Felder auf einen geladenen Körper ergibt sich die resultierende Kraft auf ihn als Vektorsumme der einzelnen Feldkräfte.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Angaben zum Lexikon

Impressum