Geladene Teilchen in magnetischen Feldern

Dabei ist Q die Ladung des Teilchens, v seine Geschwindigkeit im Magnetfeld und B die magnetische Flussdichte, durch die die Stärke des Feldes gekennzeichnet wird.
Wir betrachten nachfolgend verschiedene Fälle und setzen dabei voraus, dass die Bewegung reibungsfrei in einem homogenen magnetischen Feld, also einem Magnetfeld konstanter Stärke erfolgt.

Bewegung geladener Teilchen senkrecht zu den Feldlinien

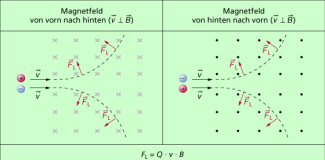
Da die Richtung der Feldlinien mit der Richtung der magnetischen Flussdichte B übereinstimmt, stehen Geschwindigkeit und magnetische Flussdichte senkrecht aufeinander (Bild 1). Aus der Gleichung für die LORENTZ-Kraft

$\begin{array}{l}{\overrightarrow{F}}_{\text{L}}=Q\cdot (\overrightarrow{v}\times \overrightarrow{B})\text{erhält man mit}\overrightarrow{v}\perp \overrightarrow{B}\text{als Betrag für}\\ \text{die Kraft}\\ F_{\text{L}}=Q\cdot v\cdot B.\end{array}$

Die Richtung der Kraft ergibt sich aus der Linke-Hand-Regel bzw. aus der Rechte-Hand-Regel (Bild 1). Da die konstante Kraft stets senkrecht zur Geschwindigkeit und senkrecht zur magnetischen Flussdichte wirkt, ruft sie eine kreisförmige Bewegung hervor. Ist das Magnetfeld hinreichend ausgedehnt, so bewegen sich die geladenen Teilchen auf Kreisbahnen, wobei die Radialkraft die LORENTZ-Kraft ist. Demzufolge kann man auch setzen:

$\begin{array}{l}{F}_r=F_L\\ m\cdot \frac{v^2}{r}=Q\cdot v\cdot B\\ \text{Stellt man die Gleichung nach dem Radius}r\text{um}\text{, so}\\ \text{erhält man für den Radius der Kreisbahn:}\\ r=\frac{m\cdot v}{Q\cdot B}\\ \text{Bewegen sich Elektronen im Magnetfeld}\text{, dann ist}Q=e\\ \text{und damit:}\\ r=\frac{m\cdot v}{e\cdot B}\text{oder}r=\frac{v}{\frac{e}{m}\cdot B}\\ v\text{Geschwindigkeit der Elektronen}\\ \frac{e}{m}\text{spezifische Ladung des Elektrons}\\ B\text{magnetische Flussdichte}\end{array}$

Der Radius der Kreisbahn ist demzufolge bei Elektronen umso kleiner, die kleiner ihre Geschwindigkeit und je größer die magnetische Flussdichte sind.

Bewegung geladener Teilchen parallel zu den Feldlinien

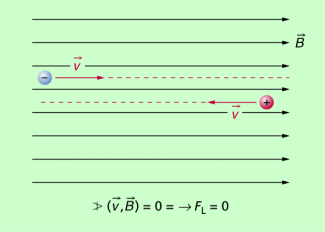
Bewegen sich geladene Teilchen parallel zu den Feldlinien, dann sind Geschwindigkeit und magnetische Flussdichte parallel zueinander (Bild 2). Der Winkel zwischen ihnen ist null. Damit ist auch der Term $\overrightarrow{v}\times \overrightarrow{B}=0\text{und damit auch}{F}_{\text{L}}=0.$
In diesem Falle werden also die geladenen Teilchen durch das magnetische Feld nicht beeinflusst. Sie bewegen sich so, wie sie sich auch ohne Magnetfeld bewegen würden.

Bewegung geladener Teilchen schräg zu den Feldlinien

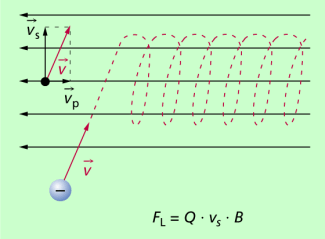
Treten geladene Teilchen schräg zu den Feldlinien in ein homogenes Magnetfeld, dann kann man die Geschwindigkeit der Teilchen in zwei Komponenten zerlegen (Bild 3): Eine Komponente hat die Richtung der Feldlinien. In dieser Richtung erfolgt keinerlei Beeinflussung der geladenen Teilchen durch das Magnetfeld. Die andere Komponente steht senkrecht zu den Feldlinien und damit auch senkrecht zur magnetischen Flussdichte. Die damit wirkende LORENTZ-Kraft hat den Betrag:
$F_{\text{L}}=Q\cdot v_s\cdot B$
Das ergibt sich auch aus der allgemeinen Gleichung für die LORENTZ-Kraft:
$\begin{array}{l}\text{Ist}\alpha \text{der Winkel zwischen}v\text{und}B,\text{dann ergibt sich aus}\\ \overrightarrow{F}=Q\cdot (\overrightarrow{v}\times \overrightarrow{B})\text{zunächst der Ausdruck}\\ F=Q\cdot v\cdot B\cdot \sin \alpha \text{oder}\\ F=Q\cdot v\cdot \sin \alpha \cdot B\\ \text{Der Term}v\cdot \sin \alpha \text{ist gleich der Geschwindigkeitskomponente}{v}_s,\\ \text{sodass man auch schreiben kann:}\\ F=Q\cdot v_s\cdot B\end{array}$
Die Geschwindigkeitskomponente senkrecht zu den Feldlinien bewirkt eine kreisförmige Bewegung geladener Teilchen. Die Geschwindigkeitskomponente parallel zu den Feldlinien führt zu einem „Auseinanderziehen“ der Kreisbahn in der betreffenden Richtung. Insgesamt kommt damit eine spiralförmige Bahn zustande, so wie sie in Bild 3 dargestellt ist.