Gewichtskräfte
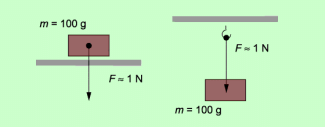
Die Gewichtskraft gibt an, wie stark ein Körper auf eine Unterlage drückt oder an einer Aufhängung zieht.
| Formelzeichen: | |
| Einheit: | ein Newton (1 N) |
Die Gewichtskraft kann mit der Gleichung berechnet werden. Sie ist wie jede andere Kraft eine gerichtete (vektorielle) Größe. Im Unterschied zur Masse ist die Gewichtskraft vom Ort abhängig, an dem sich der betreffende Körper befindet.
Ein spezieller Fall liegt vor, wenn die Kraft auf eine Unterlage oder eine Aufhängung null ist. Dann spricht man von Schwerelosigkeit oder Gewichtslosigkeit.
Alle Körper ziehen sich aufgrund ihrer Masse gegenseitig an. Diese Erscheinung wird als Massenanziehung oder Gravitation bezeichnet. Für die Erde und die auf ihr befindlichen Körper gilt dann: Alle Körper auf der Erde von dieser angezogen. Diese Anziehungskraft bewirkt, dass ein Apfel, wenn man ihn loslässt, nach unten fällt. Eine Maschine drückt auf ihre Unterlage. Ein Kind, das auf einer Schaukel sitzt, bewirkt eine Zugkraft an der Aufhängung der Schaukel. Die Kraft, mit der ein Körper aufgrund seiner Masse auf eine Unterlage drückt oder an einer Aufhängung zieht, wird als Gewichtskraft bezeichnet.
Die Gewichtskraft gibt an, wie stark ein Körper auf eine Unterlage drückt oder an einer Aufhängung zieht.
| Formelzeichen: | |
| Einheit: | ein Newton (1 N) |
Die Gewichtskraft, die auf einen Körper wirkt, hängt ab
- von seiner Masse und
- von dem Ort, an dem er sich befindet.
Je größer die Masse eines Körpers ist, umso größer ist auch seine Gewichtskraft. Sie kann berechnet werden mit der Gleichung:
| m | Masse des Körpers | |
| g | Fallbeschleunigung (Ortsfaktor) |
Die Fallbeschleunigung, auch Ortsfaktor genannt, hat auf der Erdoberfläche einen mittleren Wert von:
Das bedeutet: Ein Körper der Masse 1 kg hat auf der Erdoberfläche eine Gewichtskraft von 9,81 N. Für Abschätzungen und Überschlagsrechnungen kann man mit dem Zahlenwert 10 rechnen.
Die Gewichtskraft ist wie jede andere Kraft eine gerichtete (vektorielle) Größe. Sie zeigt in Richtung Erdmittelpunkt. Im Unterschied zur Masse ist die Gewichtskraft vom Ort abhängig, an dem sich der betreffende Körper befindet.
Gewichtskraft und Masse
Wichtige Unterschiede zwischen den physikalischen Größen Masse und Gewichtskraft sind in der nachfolgenden Übersicht zusammengestellt.
![]()
Ortsabhängigkeit der Gewichtskraft
Die Gewichtskraft ist ortsabhängig. Auf der Erdoberfläche sind die Unterschiede bei der Gewichtskraft eines Körpers gering. Der Ortsfaktor schwankt zwischen 9,79 N/kg am Äquator und 9,83 N/kg an den Polen.
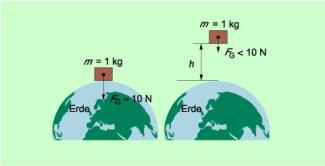
Je weiter ein Körper von der Erde entfernt ist, umso kleiner ist die Anziehungskraft der Erde und umso kleiner ist folglich auch seine Gewichtskraft (Bild 3). In einer Höhe von 250 km über der Erdoberfläche beträgt die Gewichtskraft eines Körpers von 1 kg Masse noch etwa 9 N, in 2 600 km Höhe noch etwa 5 N, also die Hälfte der Gewichtskraft auf der Erdoberfläche.
Für die Mondoberfläche hat der Ortsfaktor einen Wert von 1,62 N/kg. Demzufolge beträgt die Gewichtskraft auf der Mondoberfläche nur ca. 1/6 derjenigen auf der Erdoberfläche.
Auf der Oberfläche des größten Planeten unseres Sonnensystems, des Jupiters, beträgt die Gewichtskraft eines Körpers etwa 2,5-mal so viel wie auf der Erdoberfläche.
Gewichtskraft und Gravitationskraft
Wenn man die Gewichtskraft so definiert, wie das oben gemacht wurde, dann bedeutet das: Die Gewichtskraft eines Körpers auf der Erdoberfläche ist näherungsweise gleich der Gravitationskraft zwischen dem betreffenden Körper und der Erde. Der physikalische Hintergrund dafür ist folgender:
| - | Auf einen Körper, der auf der Erdoberfläche ruht, wirkt die Gravitationskraft der Erde, die nach folgender Gleichung berechnet werden kann: |
| - | Darüber hinaus wirkt auf jeden Körper, der sich auf der Erdoberfläche befindet, aufgrund der Rotation der Erde um ihre Achse die Fliehkraft (Zentrifugalkraft), die nach folgender Gleichung berechnet werden kann: |
Beide addieren sich, wobei allerdings die Winkelgeschwindigkeit der Erde sehr klein ist und damit der Betrag der Fliehkraft nur ca. 0,5 % der Gravitationskraft beträgt. Daher vernachlässigt man häufig die Fliehkraft und identifiziert die Gewichtskraft mit der Gravitationskraft.
Unter Schwerelosigkeit oder Gewichtslosigkeit versteht man die Erscheinung, dass z. B. Körper in einer Raumstation, die die Erde umkreist, keine Kraft auf eine Unterlage oder eine Aufhängung ausüben. Die Summe der Kräfte auf diese Körper ist null. Damit schweben sie in dem betreffenden Raum.
Ursache für die Schwerelosigkeit ist nicht die kleinere Gewichtskraft in größerer Erdentfernung - in 250 km Höhe über der Erdoberfläche beträgt die Gewichtskraft noch etwa 90 % des Wertes auf der Erdoberfläche - sondern das Zusammenwirken verschiedener Kräfte.
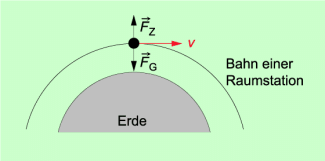
Betrachtung im mitbewegten Bezugssystem
Wir betrachten die Verhältnisse von einer Raumstation aus (Bild 5), bewegen uns also mit den Körpern mit, die wir betrachten. Auf jeden Körper in der Raumstation und auch auf die Raumstation selbst wirkt die Gewichtskraft in Richtung Erdmittelpunkt. Daneben wirkt auf jeden Körper aufgrund der Kreisbewegung um den Erdmittelpunkt eine gleich große, entgegengesetzt gerichtete Kraft, die als Fliehkraft oder Zentrifugalkraft bezeichnet wird. Sie wird nach derselben Gleichung wie die Radialkraft berechnet. Die Summe aus diesen beiden Kräften ist null. Damit ist die Gesamtkraft auf jeden Körper in der Raumstation und auch auf die Raumstation selbst null. Die Körper sind schwerelos oder, wie man auch sagt, gewichtslos. Sie schweben in der Raumstation, besitzen aber noch dieselbe Masse und dieselbe Trägheit wie auf der Erdoberfläche. Insofern ist die Bezeichnung „gewichtslos“ dem physikalischen Sachverhalt besser angepasst. Durchgesetzt hat sich aber die traditionelle Bezeichnung „schwerelos“.
Betrachtung im ruhenden Bezugssystem
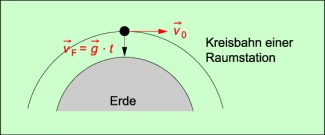
Man kann den Sachverhalt auch als Beobachter außerhalb einer Raumstation, also z.B. von der Erdoberfläche aus, beschreiben.
Die Raumstation bewegt sich tangential mit der Geschwindigkeit . Gleichzeitig fällt die Raumstation und alle Körper in ihr im freien Fall in Richtung Erde (Bild 6). Als resultierende Bewegung ergibt sich eine Kreisbewegung um die Erde herum. Auch alle Körper in der Raumstation fallen und mit ihnen die Raumstation als ihr Bezugssystem. Deshalb üben sie mit ihrer tatsächlichen Gewichtskraft keine Kraft mehr auf eine Unterlage oder eine Aufhängung aus, da diese ebenfalls frei fallen. Die Körper in der Raumstation scheinen zu schweben.
Schwerelosigkeit auf der Erde
Auf der Erde kann man Schwerelosigkeit nur kurzzeitig oder nur näherungsweise erreichen, z.B. beim Flug eines Flugzeuges auf einer parabelförmigen Bahn abwärts oder unter Wasser. Beide Möglichkeiten werden beim Training von Astronauten genutzt.
Schwerelosigkeit tritt auch bei frei fallenden Körpern auf. Das kann man experimentell einfach nachweisen. Legt man auf ein Brett ein Blatt Papier und auf dieses Papier einen Ziegelstein, so kann man das Papier nicht hervorziehen. Lässt man aber die gesamte Anordnung frei fallen, so bereitet das Wegziehen des Papiers keine Probleme, weil der frei fallende Stein auf das frei fallende Blatt Papier keine Kraft mehr ausübt.
Untersuchungen zum Verhalten von Körpern bei Schwerelosigkeit kann man also bei frei fallenden Körpern durchführen. Das wird auch genutzt, z. B. in einem Fallturm in Bremen, in dem unter den Bedingungen des freien Falls und damit der Schwerelosigkeit experimentelle Untersuchungen durchgeführt werden.
Auswirkungen der Schwerelosigkeit
Die Schwerelosigkeit in Raumstationen hat erhebliche Auswirkungen für die Raumfahrer. Aufgrund der „aufgehobenen“ Gewichtskraft kommt es zu Veränderungen im Blutkreislauf, zu Störungen der Gleichgewichtsorgane und zu Muskelschwund, vor allem bei Langzeitflügen. Auch für das Leben in der Raumstation ergeben sich wesentliche Änderungen gegenüber dem, was wir auf der Erde gewöhnt sind: Gegenstände müssen befestigt werden, sonst fliegen sie unkontrolliert herum. Beim Essen, Trinken oder Waschen müssen Flüssigkeiten abgesaugt werden, sonst verteilen sie sich unkontrolliert in der Raumstation. Es gibt kein Oben und Unten. Selbst beim Schlafen muss für eine ausreichende Befestigung gesorgt werden.
Suche nach passenden Schlagwörtern
- Schwerelosigkeit
- Rotation der Erde
- Berechnung
- Erdoberfläche
- Mondoberfläche
- Gravitationskraft
- schwerelos
- Gesamtkraft
- Masse
- Fallturm Bremen
- Raumstation
- Fliehkraft
- Gewichtskräfte
- Massenanziehung
- Gewichtslosigkeit
- Zentrifugalkraft
- Radialkraft
- Ortsfaktor
- gewichtslos
- Rechenbeispiel
- Fallbeschleunigung
- Newton