Gleichmäßig beschleunigte Drehbewegung

Eine gleichmäßig beschleunigte Drehbewegung liegt vor, wenn bei einem rotierenden starren Körper die Winkelbeschleunigung konstant und ungleich null ist. Beispiele dafür sind der Rotor eines gleichmäßig anlaufenden Elektromotors oder ein rotierendes Schwungrad, das gleichmäßig abgebremst wird. Für eine solche gleichmäßig beschleunigte Drehbewegung gelten die analogen Gesetze wie für eine gleichmäßig beschleunigte geradlinige Bewegung:
$\begin{array}{l} α = konstant \\ ω = α \cdot t + ω_{0} \\ ϕ = \frac{1}{2} α \cdot t^{2} + ω_{0} \cdot t + ϕ_{0} \end{array}$

Drehmoment

#Winkelgeschwindigkeit #Drehmoment #Radius #Drehimpuls

Ein weiteres Beispiel dafür ist das Rad eines Fahrrades bei gleichmäßiger Geschwindigkeitsänderung. Es gilt also:

Eine gleichmäßig beschleunigte Drehbewegung ist die Rotation eines starren Körpers mit einer konstanten Winkelbeschleunigung.

Bei einer Vergrößerung der Winkelgeschwindigkeit, also einer Erhöhung der Drehzahl, wird die Winkelbeschleunigung mit einem positiven Vorzeichen versehen. Eine Verringerung der Winkelgeschwindigkeit und damit eine Verkleinerung der Drehzahl wird durch eine negative Winkelbeschleunigung zum Ausdruck gebracht.

Gleichmäßig beschleunigte Drehbewegung - Maschine

L. Meyer, Potsdam

Gesetze für gleichmäßig beschleunigte Drehbewegungen

Für eine gleichmäßig beschleunigte Drehbewegung gelten die analogen Gesetze wie für eine gleichmäßig beschleunigte geradlinige Bewegung:

Die Winkelbeschleunigung ist konstant. Es gilt also:
$α = konstant$

Die Winkelgeschwindigkeit hängt von der Winkelbeschleunigung, der Zeit und der anfänglichen Winkelgeschwindigkeit (zum Zeitpunkt t = 0) ab:
$ω = α \cdot t + ω_{0}$

Der Drehwinkel ergibt sich aus Winkelbeschleunigung, Winkelgeschwindigkeit und Zeit:
$\begin{array}{l} ϕ = \frac{1}{2} α \cdot t^{2} + ω_{0} \cdot t + ϕ_{0} \\ α Winkelbeschleunigung \\ t Zeit \\ ω_{0} anfängliche Winkelgeschwindigkeit \\ ϕ_{0} anfänglicher Drehwinkel \end{array}$

Bei Berechnungen sind die oben genannten Vorzeichenregeln zu beachten.

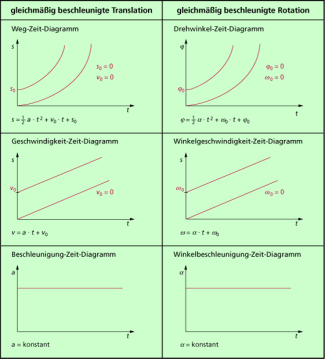
$\begin{array}{l} Ist z . B . der anfängliche Drehwinkel ϕ_{0} = 0 \\ und wird ein Schwungrad mit bestimmter Winkel- \\ geschwindigkeit ω_{0} gleichmäßig abgebremst, so \\ gilt für den Drehwinkel die Gleichung: \\ ϕ = - \frac{1}{2} α \cdot t^{2} + ω_{0} \cdot t \end{array}$

Die genannten Zusammenhänge lassen sich auch grafisch darstellen (Bild 2). Die Diagramme für die gleichmäßig beschleunigte Rotation entsprechen denen für die analogen Größen bei einer gleichmäßig beschleunigten geradlinigen Bewegung. Sie sind in Bild 2 gegenübergestellt.

Physik Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Physik kostenlos lernen

Verwandte Artikel

Gleichmäßig beschleunigte Drehbewegung

Drehmoment

Gesetze für gleichmäßig beschleunigte Drehbewegungen

Rechtliches

Einloggen