Mechanische Energie und ihre Erhaltung in Physik | Schülerlexikon

Erklärvideos und Übungen zur Mechanischen Energieumwandlung gibt es hier!

Mechanische Energie und ihre Formen

Benannt sind die Einheiten nach den Naturwissenschaftlern JAMES PRESCOTT JOULE (1818-1889) und ISAAC NEWTON (1643-1727). Es gilt:

$1 J = 1 Nm = 1 \frac{kg \cdot m^{2}}{s^{2}}$

Vielfache der Einheit 1 J sind ein Kilojoule (1 kJ), ein Megajoule (1 MJ) und ein Gigajoule (1 GJ):

1 kJ	= 1 000 J
1 MJ	= 1 000 kJ	= 1 000 000 J
1 GJ	= 1 000 MJ	= 1 000 000 kJ	= 1 000 000 000 J

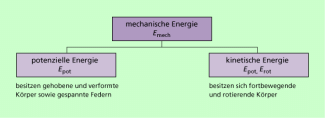
Mechanische Energie kennzeichnet den Zustand eines Körpers. Sie wird deshalb auch als Zustandsgröße bezeichnet. Sie kann in andere Energieformen umgewandelt und von einem Körper auf andere Körper übertragen werden. Spezielle Formen mechanischer Energie sind die potenzielle Energie (Energie der Lage) und die kinetische Energie (Energie der Bewegung), die ihrerseits wieder in verschiedenen Formen auftreten können, wie die nachfolgende Übersicht zeigt.

Die potenzielle Energie

Gehobene Körper, z. B. eine an einem Kranhaken hängende Betonplatte oder die Kinder auf dem Ast (Bild 2), besitzen potenzielle Energie. Sie ist eine Form mechanischer Energie. Ebenfalls potenzielle Energie haben z.B. eine gespannte Feder, ein verbogener Ast oder der gebogene Sprungstab eines Stabhochspringers. Statt von potenzieller Energie spricht man auch von Energie der Lage oder Lageenergie.
Zwei spezielle Fälle potenzieller Energie sind die potenzielle Energie eines gehobenen Körpers in der Nähe der Erdoberfläche und die potenzielle Energie einer gespannten Feder.
Potenzielle Energie eines gehobenen Körpers: Die potenzielle Energie eines gehobenen Körpers in der Nähe der Erdoberfläche ist von der Masse des Körpers und von seiner Höhe bezüglich einer willkürlich gewählten Ausgangshöhe abhängig. Sie kann berechnet werden mit den Gleichungen:

Übersicht über Formen mechanischer Energie

$\begin{array}{l} E_{pot} = F_{G} \cdot h \\ E_{pot} = m \cdot g \cdot h \\ F_{G} Gewichtskraft des Körpers \\ h Höhe \\ m Masse des Körpers \\ g Fallbeschleunigung (Ortsfaktor) \end{array}$

Bei größerer Entfernung von der Erdoberfläche ist zu beachten, dass sich die Fallbeschleunigung mit der Höhe über der Erdoberfläche ändert.

Material zum Thema

BWS-PHY2-0211-05.mcd

BWS-PHY2-0211-05.mcd

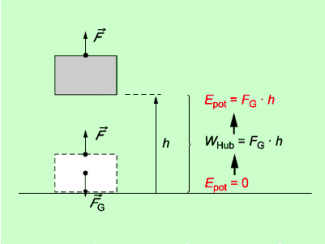
Die potenzielle Energie ist genau so groß wie die Hubarbeit, die zum Heben des Körpers in die Höhe h erforderlich ist (Bild 3). Dabei ist zu beachten, dass man die Höhe h stets auf eine bestimmte Ausgangshöhe (Bezugsniveau) null beziehen muss. Was man als Bezugsniveau wählt, hängt häufig von der Zweckmäßigkeit ab.

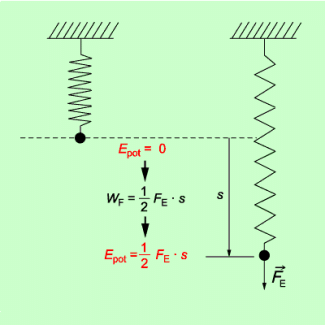
Potenzielle Energie einer gespannten Feder: Die potenzielle Energie einer gespannten Feder hängt von der Härte der Feder und davon ab, wie weit sie gedehnt ist. Sie ist umso größer,

je härter die Feder und damit je größer die Federkonstante ist und
je stärker die Feder gedehnt wird.

Die potenzielle Energie einer gespannten Feder kann berechnet werden mit den Gleichungen:

$\begin{array}{l} E_{pot} = \frac{1}{2} F_{E} \cdot s \\ E_{pot} = \frac{1}{2} D \cdot s^{2} \\ F_{E} maximale Kraft (Endkraft) \\ s Dehnung (Verlängerung) der Feder \\ D Federkonstante (D = F / s) \end{array}$

Material zum Thema

BWS-PHY2-0211-08.mcd

BWS-PHY2-0211-08.mcd

Sie ist genau so groß wie die zuvor an ihr verrichtete Verformungsarbeit (Federspannarbeit).

In der nachfolgenden Übersicht sind einige Werte für die potenzielle Energie von Körpern in Natur und Technik angegeben.

Potenzielle Energie in Natur und Technik
Feder (D = 0,2 N/cm), um 10 cm gedehnt	0,01 J
Tafel Schokolade (m = 100 g), um 1 m gehoben	1 J
Ziegelstein (m = 3,5 kg), um 1 m gehoben	35 J
Mensch (m = 55 kg) auf 10-m-Sprungturm	5 500 J = 5,5 kJ
Rammbär (m = 1 000 kg), um 1 m gehoben	10 000 J = 10 kJ
Flugzeug (m = 100 t) in 1 km Höhe	$9,8 \cdot 10^{8} J$

Zusammenhang zwischen der potenziellen Energie eines Körpers und der an ihm verrichteten Hubarbeit

Die kinetische Energie

Sich bewegende Körper, z. B. Radfahrer, ein fahrendes Auto, ein fallender Stein oder ein rotierendes Schwungrad besitzen kinetische Energie. Statt von kinetischer Energie spricht man auch von Energie der Bewegung oder Bewegungsenergie. Bei rotierenden Körpern nennt man die kinetische Energie Rotationsenergie.

Kinetische Energie bei der Translation: Die kinetische Energie eines sich fortbewegenden Körpers hängt von seiner Masse bzw. seiner Geschwindigkeit ab. Sie ist umso größer,

je größer die Masse des Körpers ist und
je größer seine Geschwindigkeit ist.

Sie kann berechnet werden mit der Gleichung:
$\begin{array}{l} E_{kin} = \frac{1}{2} m \cdot v^{2} \\ m Masse des Körpers \\ v Geschwindigkeit des Körpers \end{array}$

Zusammenhang zwischen der potenziellen Energie einer gespannten Feder und der an ihr verrichteten Federspannarbeit.

Material zum Thema

BWS-PHY2-0211-13.mcd

BWS-PHY2-0211-13.mcd

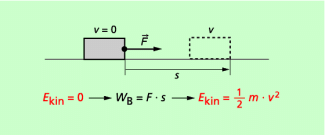
Sie ist genau so groß wie die Beschleunigungsarbeit, die erforderlich ist, um dem Körper die Geschwindigkeit v zu verleihen (Bild 5). Dabei ist zu beachten, dass sich die Geschwindigkeit v stets auf ein bestimmtes Bezugssystem bezieht. So hat z. B. eine Person, die in einem fahrenden Auto sitzt, gegenüber dem Auto die kinetische Energie null, weil ihre Geschwindigkeit gegenüber dem Auto null ist. Gegenüber der Straße ist aber die kinetische Energie größer als null, da sich das Auto und damit auch die Person in ihm bezüglich der Straße mit einer bestimmten Geschwindigkeit bewegt.
Gerade bei Fahrzeugen ist zu beachten, dass die kinetische Energie mit dem Quadrat der Geschwindigkeit wächst. Das bedeutet: Eine Verdopplung der Geschwindigkeit eines Autos bedeutet eine Vervierfachung seiner kinetischen Energie. Das ist bei Unfällen von entscheidender Bedeutung.

Kinetische Energie in Natur und Technik
Apfel (m = 100 g) nach 1 m freien Fall	1 J
Fußgänger (m = 55 kg) bei 5 km/h	50 J
Radfahrer (m = 75 kg) bei 20 km/h	1 200 J
PKW (m = 1 000 kg) bei 50 km/h	96 000 J = 96 kJ
PKW (m = 1 000 kg) bei 100 km/h	386 000 J = 386 kJ
ICE (m = 500 t) bei 180 km/h	625 MJ
Jumbo-Jet (m = 320 t) beim Abheben (310 km/h)	1 200 MJ

Kinetische Energie bei der Rotation: Auch rotierende Körper, z. B. sich drehende Schwungräder, ein rotierender Schleifstein oder ein rotierendes Karussell, besitzen kinetische Energie, die auch als Rotationsenergie bezeichnet wird.
Die Rotationsenergie eines Körpers hängt ab von der Drehzahl und davon, wie sich die Masse des Körpers bezüglich der Drehachse verteilt. Sie ist umso größer,

je größer die Winkelgeschwindigkeit (Drehzahl) des Körpers ist,
je größer seine Masse ist und
je weiter die Masse von der Drehachse entfernt ist.

Die letzten beiden Einflussfaktoren werden durch die physikalische Größe Trägheitsmoment erfasst. Für die Rotationsenergie gilt:

$\begin{array}{l} E_{kin} = E_{rot} = \frac{1}{2} J \cdot ω^{2} \\ J Trägheitsmoment des Körpers \\ ω Winkelgeschwindigkeit um eine \\ Drehachse \end{array}$

Schwungräder, in denen kinetische Energie gespeichert werden soll, baut man deshalb so, dass sie eine große Masse haben und sich der größte Teil der Masse relativ weit von der Drehachse entfernt befindet.

Material zum Thema

BWS-PHY2-0211-16.mcd

BWS-PHY2-0211-16.mcd

Energieerhaltungssatz der Mechanik

Der Energieerhaltungssatz der Mechanik ist ein spezieller Fall des allgemeinen Energieerhaltungssatzes. Er lautet:

In einem abgeschlossenen System gilt unter der Bedingung, dass keine Umwandlung von mechanischer Energie in andere Energieformen erfolgt:
Die Summe aller potenziellen und kinetische Energien ist konstant.

$\begin{array}{l} E_{pot} + E_{kin} = konstant oder \\ Δ (E_{pot} + E_{kin}) = 0 \end{array}$

Dieser spezielle Energieerhaltungssatz hat nur eine relativ geringe „Anwendungsbreite“. Das hängt damit zusammen, dass in vielen Fällen nur kurzzeitig die gesamte mechanische Energie als konstant angesehen werden kann, weil meist durch Reibung mechanische Energie in nichtmechanische Energieformen (thermische Energie bzw. innere Energie) umgewandelt wird. Bei seiner Anwendung ist also stets zu prüfen, ob seine Gültigkeitsbedingungen zumindest annähernd erfüllt sind.

Beispiele für die Anwendung des Energieerhaltungssatzes der Mechanik

Für einige spezielle Fälle kann der Energieerhaltungssatz der Mechanik genutzt werden, um Sachverhalte zu erklären und physikalische Größen zu berechnen. Wir betrachten nachfolgend drei ausgewählte Beispiele.

(1) Umwandlung mechanischer Energieformen ineinander

Erkläre, weshalb eine aus bestimmter Höhe auf ein Trampolin treffende Person annähernd wieder die gleiche Höhe erreicht!

In einer bestimmten Höhe besitzt eine Person potenzielle Energie gegenüber dem Trampolin. Beim Fall wird diese potenzielle Energie in kinetische Energie umgewandelt. Das Trampolin wird elastisch verformt und wirkt so, dass die Person wieder nach oben geschleudert wird. Dabei wird kinetische Energie in potenzielle Energie umgewandelt. Da bei diesem Vorgang nur wenig mechanische Energie in thermische Energie umgewandelt wird, erreicht die Person nach dem Energieerhaltungssatz der Mechanik näherungsweise wieder die gleiche Höhe.

(2) Geschwindigkeit beim freien Fall

Eine Person springt aus 5 m Höhe ins Wasser. Mit welcher Geschwindigkeit trifft sie auf der Wasseroberfläche auf?

Analyse:
Die Person besitzt zunächst potenzielle Energie. Diese wird beim Sprung fast vollständig in kinetische Energie umgewandelt. Die Reibung (Luftwiderstand) kann in diesem Fall vernachlässigt werden.

Gesucht:

Gegeben:

v

h = 5 m
$g = 9,81 \frac{m}{s^{2}}$

Lösung:

$\begin{array}{l} m \cdot g \cdot h = \frac{1}{2} m \cdot v^{2} \\ g \cdot h = \frac{1}{2} v^{2} \\ v = \sqrt{2 g \cdot h} \\ v = \sqrt{2 \cdot 9,81 \frac{m}{s^{2}} \cdot 5 m} \\ v = 9,9 \frac{m}{s^{2}} = 36 \frac{km}{h} \end{array}$

Ergebnis:
Eine Person, die aus 5 m Höhe springt, trifft mit einer Geschwindigkeit von 36 km/h auf der Wasseroberfläche auf.
Beachte: Die Geschwindigkeit ist unabhängig davon, ob die Person eine große oder eine kleine Masse hat.

(3) Höhe bei bestimmter Abwurfgeschwindigkeit

Ein Stein wird mit einer Geschwindigkeit von 10 m/s senkrecht nach oben geworfen. Welche maximale Höhe erreicht er?

Analyse:
Die kinetische Energie des Steines wird in potenzielle Energie umgewandelt. Im höchsten Punkt seiner Bahn ist die kinetische Energie null, die potenzielle Energie maximal. Die Reibung kann für diesen Vorgang vernachlässigt werden.

Gesucht:
Gegeben:

h
v = 10 m/s

g = 9,81 \frac{m}{s^{2}}

Lösung:

$\begin{array}{l} \frac{1}{2} m \cdot v^{2} = m \cdot g \cdot h \\ \frac{1}{2} v^{2} = g \cdot h \\ h = \frac{v^{2}}{2 g} \\ h = \frac{{(10 \frac{m}{s})}^{2}}{2 \cdot 9,81 \frac{m}{s^{2}}} \\ h = 5,1 m \end{array}$

Ergebnis:
Bei einer Abwurfgeschwindigkeit von 10 m/s erreicht der Stein eine maximale Höhe von 5,1 m.
Beachte: Die maximale Höhe hängt nur von der Anfangsgeschwindigkeit ab. Sie ist unabhängig davon, welche Masse der Körper hat.

Zusammenhang zwischen der kinetischen Energie bei der Translation und der Beschleunigungsarbeit

Formelzeichen:	$E_{mech}$
Einheiten:	ein Joule (1 J) ein Newtonmeter (1 Nm)

Mechanische Energie und ihre Erhaltung

Umwandlung mechanischer Energie

Mechanische Energie und ihre Formen

Die potenzielle Energie

BWS-PHY2-0211-05.mcd

BWS-PHY2-0211-08.mcd

Die kinetische Energie

BWS-PHY2-0211-13.mcd

BWS-PHY2-0211-16.mcd

Energieerhaltungssatz der Mechanik

Beispiele für die Anwendung des Energieerhaltungssatzes der Mechanik

Rechtliches

Einloggen