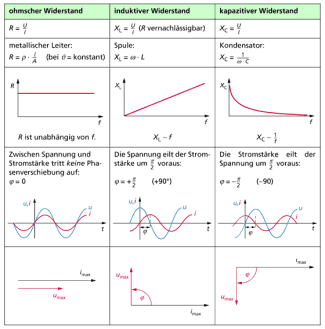
Ohmsche, induktive und kapazitive Widerstände im Wechselstromkreis

Der elektrische Widerstand

In einem Gleichstromkreis mit einer Gleichspannungsquelle konstanter Spannung haben die zu verschiedenen Zeitpunkten an einem Bauelement gemessenen Größen U und I immer den gleichen Wert. Es ist deshalb möglich, mit ihrer Hilfe ein Maß für die strombegrenzende Wirkung des gesamten Kreises zu definieren. Man nennt diese Größe den elektrischen Widerstand mit dem Kurzzeichen R (von Rheostat) und definiert:
$R=\frac{U}{I}$
Der elektrische Widerstand hat ebenso wie U und I zu einem bestimmten Zeitpunkt einen bestimmten Wert. Der reziproke Wert des Widerstandes wird als elektrische Leitfähigkeit bezeichnet. Elektrischer Widerstand bzw. elektrische Leitfähigkeit sind nur vom Aufbau des Leiters (Länge, Querschnittsfläche, Stoff) abhängig. Für metallische Leiter gilt das Widerstandsgesetz:

$\begin{array}{l}R=\rho \cdot \frac{l}{A}\\ \rho \text{spezifischer elektrischer Widerstand}\\ l\text{Länge des Leiters}\\ A\text{Querschnittsfläche des Leiters}\end{array}$

Solche Gleichstromwiderstände werden auch als ohmsche Widerstände bezeichnet.

Wechselstromwiderstände

Unter einem Wechselstromkreis versteht man einen Stromkreis, in dem sich die Polarität der elektrischen Quelle periodisch so ändert, dass sich auch die Flussrichtung periodisch ändert. Wir beschränken uns auf die Betrachtung von sinusförmigem Wechselstrom. Wie im Gleichstromkreis bilden auch im Wechselstromkreis ohmsche Widerstände ein Hindernis für den Strom, also einen elektrischen Widerstand. Darüber hinaus verhalten sich im Wechselstromkreis auch Kondensatoren und Spulen wie elektrische Widerstände. Man bezeichnet sie mit dem Oberbegriff Wechselstromwiderstände.

Ohmsche Widerstände

Bauelemente, die im Gleichstromkreis einen konstanten Widerstandswert besitzen und in denen die elektrische Energie ausnahmslos in nichtelektrische Formen (thermische Energie, Lichtenergie) umgewandelt wird, besitzen den gleichen Widerstandswert im Wechselstromkreis. Es gilt also:
$R_{=}=R_{\approx }\text{mit}{R}_{=}=R_{\approx }=\frac{U}{I}$
Derartige Bauelemente nennt man ohmsche Widerstände oder Wirkwiderstände. Zu ihnen gehören alle Drahtwiderstände, also z.B. auch der Widerstand, den der Draht einer Spule hat.

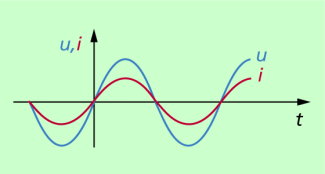
Untersucht man experimentell den zeitlichen Verlauf von Spannung und Stromstärke an einem solchen ohmschen Widerstand, dann zeigt sich, dass Spannung und Stromstärke in Phase sind (Bild 3). Das bedeutet: Spannung und Stromstärke erreichen zu gleichen Zeitpunkten den Wert null oder den Maximalwert. Zwischen Spannungskurve und Stromstärkekurve gibt es keine Phasenverschiebung oder einfacher: Die Phasenverschiebung zwischen Spannung und Stromstärke ist null.

Induktive Widerstände

Untersucht man den elektrischen Widerstand einer Spule im Gleichstromkreis und im Wechselstromkreis, dann zeigt sich: Der elektrische Widerstand der Spule ist im Wechselstromkreis wesentlich größer als im Gleichstromkreis. Ursache dafür ist die Selbstinduktion. Die im Wechselstromkreis in der Spule entstehende Selbstinduktionsspannung und der mit ihr verbundene Selbstinduktionsstrom ist nach dem lenzschen Gesetz so gerichtet, dass er der ursprünglichen Stromstärke entgegenwirkt und sie somit schwächt. Damit wirkt eine Spule aufgrund der Selbstinduktion wie ein Widerstand. Dieser Widerstand wird als induktiver Widerstand bezeichnet. Da dem Stromkreis durch diesen Widerstand keine Energie entzogen wird, bezeichnet man einen induktiven Widerstand auch als Blindwiderstand. Für den induktiven Widerstand gilt:

$\begin{array}{l}{X}_{\text{L}}=\omega \cdot L=2\pi \cdot f\cdot L\\ \omega \text{Kreisfrequenz}\\ L\text{Induktivität der Spule}\\ f\text{Frequenz des Wechselstromes}\end{array}$

Neben diesem induktiven Widerstand aufgrund der Selbstinduktion hat eine Spule auch immer noch den ohmschen Widerstand des Spulendrahtes, der aber in der Regel deutlich kleiner ist als der induktive Widerstand. Das gilt insbesondere für Spulen mit Eisenkern. Wie die verschiedenen Wechselstromwiderstände zusammenwirken, ist in gesonderten Beiträgen unter den Titeln „Reihenschaltung von Wechselstromwiderständen“ und „Parallelschaltung von Wechselstromwiderständen“ zu finden.

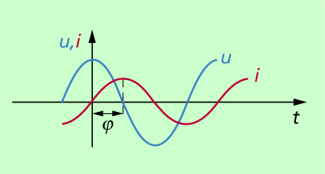
Untersucht man den zeitlichen Verlauf von Spannung und Stromstärke an einem solchen induktiven Widerstand, dann zeigt sich: An einer Spule eilt die Spannung der Stromstärke um 90° oder T/4 voraus (Bild 4). Es besteht also zwischen Spannung und Stromstärke eine Phasendifferenz. Der genannte Wert von 90° gilt für einen reinen induktiven Widerstand und näherungsweise für eine Spule, wenn deren induktiver Widerstand wesentlich größer als ihr ohmscher Widerstand ist.

Kapazitive Widerstände

Schaltet man einen Kondensator in einen Gleichstromkreis, so lädt er sich zwar auf, bildet aber dann einen unendlich großen Widerstand. Im Wechselstromkreis kommt es dagegen zu einem ständigen Auf- und Entladen. Ein Kondensator verhindert den Stromfluss nicht mehr. Er wirkt vielmehr wie ein elektrischer Widerstand. Dieser Widerstand wird maßgeblich durch die Kapazität des Kondensators bestimmt. Daher ist die Bezeichnung kapazitiver Widerstand üblich. Da dem Stromkreis durch diesen Widerstand keine Energie entzogen wird, bezeichnet man einen kapazitiven Widerstand ebenso wie einen induktiven Widerstand auch als Blindwiderstand. Für den kapazitiven Widerstand gilt:

$\begin{array}{l}{X}_{\text{C}}=\frac{1}{\omega \cdot C}=\frac{1}{2\pi \cdot f\cdot C}\\ \omega \text{Kreisfrequenz}\\ C\text{Kapazität des Kondensators}\\ f\text{Frequenz des Wechselstromes}\end{array}$

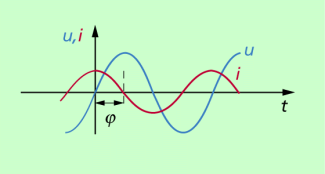
Untersucht man den zeitlichen Verlauf von Spannung und Stromstärke an einem solchen induktiven Widerstand, dann zeigt sich: An einem Kondensator eilt die Stromstärke der Spannung um 90° oder T/4 voraus (Bild 5). Es besteht also zwischen Spannung und Stromstärke eine Phasendifferenz von 90° oder T/4.

Vergleich von ohmschem, induktivem und kapazitivem Widerstand

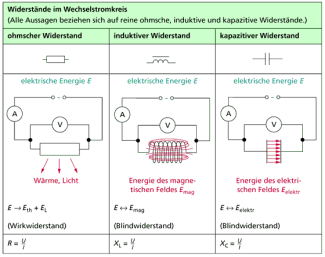
Die Gemeinsamkeiten und Unterschiede zwischen den drei Wechselstromwiderständen werden besonders durch einen unmittelbaren Vergleich deutlich, so wie er in den Bildern 6 und 7 dargestellt ist.
In Bild 6 sind neben den Schaltzeichen die energetischen Verhältnisse dargestellt. Während der ohmsche Widerstand eines Bauelementes auf der Umwandlung von elektrischer Energie in Wärme und Licht beruht, sind induktiver und kapazitiver Widerstand mit keiner Energieumwandlung in nichtelektrische Energieformen verknüpft - daher auch die Bezeichnung
Blindwiderstand. Vielmehr „pendelt“ die Energie zwischen der Quelle und dem Bauelement hin und her. Beim induktiven Widerstand wird elektrische Energie der Quelle in Energie des Magnetfeldes der Spule umgewandelt und umgekehrt. Beim kapazitiven Widerstand wird elektrische Energie der Quelle in Energie des elektrischen Feldes des Kondensators umgewandelt und umgekehrt.
Daher ist man bestrebt, dort, wo in Wechselstromkreisen der Einsatz eines Widerstandes erforderlich ist, nach Möglichkeit verlustlose Blindwiderstände zum Einsatz zu bringen. Spulen, die zu diesem Zweck verwandt werden, nennt man Drosselspulen .

Die Möglichkeiten der Berechnung der Widerstände, ihre Frequenzabhängigkeit und die Phasenlage zwischen Spannung und Stromstärke sind in Bild 7 angegeben. Die Phasenlage zwischen Spannung und Stromstärke lässt sich im Zeigerdiagramm darstellen (Bild 7 unten). Dazu ordnet man der Stromstärke zu einem bestimmten Zeitpunkt die waagerechte Richtung nach links zu und zeichnet die Phasenlage der Spannung entsprechend ein. Die Vorzeichen entsprechen der mathematischen Festlegung des Drehsinns entgegen der Uhrzeigerrichtung.

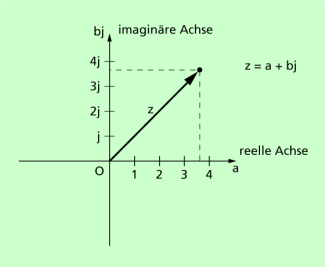
Darstellung der Wechselstromgrößen mithilfe komplexer Zahlen

Die folgenden Ausführungen können demjenigen, der Kenntnisse über komplexe Zahlen hat, zu einem besseren Verständnis der Beschreibungen der Vorgänge im Wechselstromkreis verhelfen.
Zur Schreibweise: Eine komplexe Zahl wird durch Unterstreichung gekennzeichnet, die imaginäre Einheit wird - um Verwechslungen zu vermeiden - durch j dargestellt. $\underset{¯}{z}=a+bj$ und a,b reell. Die zu $\underset{¯}{z}$ konjugiert komplexe Zahl wird mit ${\underset{¯}{z}}^{*}$ bezeichnet. Es gilt $\underset{¯}{z}\cdot {\underset{¯}{z}}^{*}=a^2+b^2$.
Nach Bild 8 kann man eine komplexe Zahl auch darstellen durch $\underset{¯}{z}=r(\cos \phi +j\sin \phi )\text{mit}r=\sqrt{\underset{¯}{z}\cdot {\underset{¯}{z}}^{*}}$. Insbesondere gilt die Darstellung durch die Exponentialfunktion: $\underset{¯}{z}=r\cdot e^{j\phi }=r(\cos \phi +j\cdot \sin \phi )$.

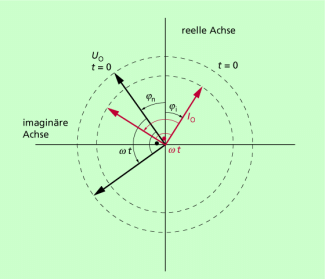
Man benutzt die komplexe Darstellung, um über deren Realteil die zeitlichen Verläufe von u und i darzustellen. Da der Realteil eine Kosinusfunktion enthält, dreht man die gaußsche Ebene im Ursprung um 90°. Somit kann mit den rotierenden Zeigern in der üblichen Darstellung der Graph der Stromstärke oder Spannungskurve gezeichnet werden (Bild 9).
Weil Kosinus- und Sinusfunktion nur durch eine Verschiebung entlang der Abszissenachse zur Deckung gebracht werden können, erhält man bei geeigneter Größe des Nullphasenwinkels die Darstellung der Sinusfunktion.
Zur komplexen Darstellung einer sinusförmigen Wechselspannung nehmen wir an, dass der Pfeil zum Zeitpunkt t um den Winkel $\omega \cdot t+\phi {}_{\text{u}}$ in der gaußschen Ebene gegen die reelle Achse gedreht sei. Dabei ist $\phi {}_{\text{u}}$ die Anfangslage für t = 0 (Nullphasenwinkel). Hat die Wechselspannung die Amplitude $U_0$, lautet die komplexe Darstellung: $\begin{array}{l}{U}_0\cdot e^{j(\omega \cdot t+{\phi }_u)}=U_0\cdot e^{j\omega \cdot t}\cdot e^{j{\phi }_u}=U_0\cdot e^{j{\phi }_u}\cdot e^{j\omega t}=\underset{¯}{U}{e}^{j\omega t},\\ \text{wobei}\underset{¯}{U}{e}^{j\omega t}=\text{konstant die komplexe Amplitude ist}\text{.}\end{array}$
Analog hierzu lässt sich die Stromstärke darstellen als: $I_0\cdot e^{j(\omega t+{\phi }_i)}=I_0\cdot e^{j{\phi }_i}\cdot e^{j\omega t}=\underset{¯}{I}{e}^{j\omega t}$

Mit dieser Darstellung lässt sich zeigen, dass bei beliebiger Phasenlage von Stromstärke und Spannung gegeneinander der Quotient aus den Augenblickswerten eine Konstante, eben den Wechselstromwiderstand Z liefert.
$\begin{array}{l}\frac{U_0\cdot e^{j(\omega t+{\phi }_u)}}{I_0\cdot e^{j(\omega t+{\phi }_i)}}=\frac{\underset{¯}{U}\cdot e^{j\omega t}}{\underset{¯}{I\cdot }{e}^{j\omega t}}=\frac{\underset{¯}{U}}{\underset{¯}{I}}=\frac{U_0\cdot e^{j{\phi }_u}}{I_0\cdot e^{j{\phi }_i}}\\ =\frac{U_0}{I_0}\cdot e^{j({\phi }_u-{\phi }_i)}=\frac{U_0}{I_0}{e}^{j\phi }=\underset{¯}{Z}=\text{konstant}\end{array}$
$\begin{array}{l}\text{Der Betrag von}\underset{¯}{Z}\text{ergibt sich zu}\left|\underset{¯}{Z}\right|=\frac{U_0}{I_0}\\ \text{mit dem Nullphasenwinkel}\phi ={\phi }_u-{\phi }_i.\end{array}$
Da bei einer derartigen Quotientenbildung stets der zeitabhängige Anteil $\omega \cdot t$ herausfällt, kann man auch mit ruhenden Zeigern arbeiten.
Man gibt je nach Anwendungsfall dem Nullphasenwinkel des Stromes oder der Spannung den Wert null vor. Dann liegt bei ${\phi }_i=0$ der Stromzeiger auf der reellen Achse, der Spannungszeiger ist um $\phi ={\phi }_u-0={\phi }_u$ dagegen gedreht.
Addieren sich etwa zwei Spannungen ${\underset{¯}{U}}_1\text{und}{\underset{¯}{U}}_1\text{zu einer Gesamtspannung}\underset{¯}{U}={\underset{¯}{U}}_1+{\underset{¯}{U}}_2,$
so werden die komplexen Zeiger geometrisch addiert.

Zwei Folgerungen aus der komplexen Darstellung seien noch hervorgehoben:
Für den Spannungsabfall über einer idealen Spule gilt $u=L\frac{\text{d}i}{\text{d}t}$.
Ist der Strom ein sinusförmiger Wechselstrom, so gilt:
$\begin{array}{l}\underset{¯}{U\cdot }{e}^{j\omega t}=L\frac{\text{d}(\underset{¯}{I}\cdot e^{j\omega t})}{\text{d}t}=j\omega \cdot L\underset{¯}{\cdot I\cdot }{e}^{j\omega t}\\ \text{Daraus wird}\underset{¯}{Z}=j\omega \cdot L,\text{also}Z=\frac{U_0}{I_0}=\omega \cdot L\end{array}$

Da wegen der Ableitung u und i um $\frac{\pi }{2}$ phasenverschoben sind, gilt: $\phi ={\phi }_u-{\phi }_i=\frac{\pi }{2}$

An einem Kondensator gilt $C=\frac{Q}{U}$.
Wie bereits für die Berechnung der Ladung genutzt, ist $Q={\displaystyle \int i\text{d}t}$. Setzt man hier wieder die komplexen Darstellungen ein, erhält man: $\underset{¯}{U}\cdot e^{j\omega t}=\frac{1}{C}{\displaystyle \int \underset{¯}{I}}\cdot e^{j\omega t}dt=\frac{1}{j\omega \cdot C}\underset{¯}{I\cdot }{e}^{j\omega t}$
Das liefert den komplexen Widerstand $\underset{¯}{Z}=\frac{1}{j\omega \cdot C}=-\frac{j}{\omega \cdot C}$.
Dessen Betrag ist $Z=\frac{1}{\omega \cdot C}$.
Da die Sinusfunktion des Stromes integriert wird, ist die Spannung dagegen um $\frac{\pi }{2}$ phasenverschoben. Auch weist der Zeiger für den komplexen Widerstand auf der imaginären Achse nach unten: $\phi ={\phi }_u-{\phi }_i=-\frac{\pi }{2}$.