Reihenschaltung von Wechselstromwiderständen

Unter Wechselstromwiderständen versteht man ohmsche, induktive und kapazitive Widerstände. Für die Reihenschaltung solcher Widerstände gelten im Wechselstromkreis andere Gesetze als für Widerstände im Gleichstromkreis. Der Gesamtwiderstand Z, der auch als Scheinwiderstand bezeichnet wird, kann bei Reihenschaltung von Wechselstromwiderständen berechnet werden mit der Gleichung:

Z = R 2 + ( X L − X C ) 2 oder Z = R 2 + ( ω ⋅ L − 1 ω ⋅ C ) 2

Für die Spannungsverteilung gilt, dass die Summe der Teilspannungen größer ist als die Spannung der anliegenden Spannungsquelle.

Reale und reine Wechselstromwiderstände

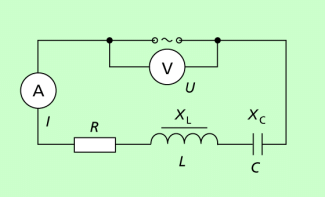
Unter Wechselstromwiderständen versteht man ohmsche, induktive und kapazitive Widerstände. Für die Reihenschaltung solcher Widerstände (Bild 1) gelten im Wechselstromkreis andere Gesetze als für Widerstände im Gleichstromkreis. Wir betrachten dabei reine Widerstände der jeweiligen Art. Das bedeutet beispielsweise für eine Spule: Eine reale Spule hat sowohl einen induktiven als auch einen ohmschen Widerstand und kann damit als Reihenschaltung eines rein induktiven und eines rein ohmschen Widerstandes angesehen werden. Wir betrachten nur den induktiven Anteil des Widerstandes, also die Spule als rein induktiven Widerstand. Analog wird beim ohmschen Widerstand und kapazitiven Widerstand verfahren, denn auch ein ohmscher Widerstand kann einen induktiven Anteil haben. Während man im Fall des Drahtwiderstandes unmittelbar die spulenartigen Drahtwindungen sieht, bleibt das bei Schichtwiderständen meist verborgen. Tatsächlich wird auf einem Träger eine leitende Schicht aufgetragen, aus der durch einen spiralig umlaufenden Fräsvorgang leitendes Material abgetragen wird, so dass eine wendelartig umlaufende Schicht übrig bleibt. Auf diese Weise wird der geforderte Widerstandswert erzeugt. Es ist unmittelbar einzusehen, dass dieser spulenartige Aufbau zu einem induktiven Anteil führt. Dieser ist allerdings in der Regel so klein, dass man ihn vernachlässigen kann. Trotzdem gilt:

Die allgemeine Behandlung der Zusammenschaltung beliebiger Wechselstromwiderstände ist mit den in der Schule zur Verfügung stehenden mathematischen Kenntnisse nicht möglich und auch nicht erforderlich.

Nachfolgend ist der vereinfachte Fall der Reihenschaltung von einem rein ohmschen, induktiven und kapazitiven Widerstand dargestellt.

Reihenschaltung von Wechselstromwiderständen

Es werden ein ohmscher Widerstand R (Wirkwiderstand), ein induktiver Widerstand X L und ein kapazitiver Widerstand X C in Reihe geschaltet, so wie es Bild 1 zeigt. Induktiver und kapazitiver Widerstand werden auch als Blindwiderstand bezeichnet. Den Gesamtwiderstand im Wechselstromkreis nennt man Scheinwiderstand Z.
Für eine solche Reihenschaltung gilt zunächst wie im Gleichstromkreis, dass die Stromstärke im Stromkreis überall den gleichen Wert hat.

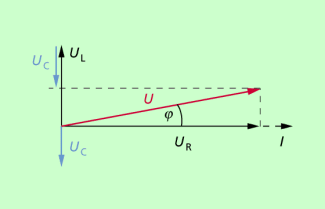
Um die Verhältnisse bei den Spannungen zu klären, stellt man die Teilspannungen an den einzelnen Bauelementen in einem Zeigerdiagramm dar (Bild 2). Als Bezugsrichtung (x-Richtung von links nach rechts) wird die Richtung des Stromstärke-Zeigers am ohmschen Widerstand gewählt. Die Richtung des Spannungs-Zeigers am ohmschen Widerstand ist die gleiche, da am ohmschen Widerstand keine Phasenverschiebung zwischen Spannung und Stromstärke auftritt. Am induktiven Widerstand eilt die Spannung dem Strom um 90° voraus. Dementsprechend wird die Spannung am induktiven Widerstand nach oben abgetragen (Bild 2). Bezogen auf den Stromzeiger ist der Spannungszeiger am kapazitiven Widerstand um 90° verzögert. Dementsprechend wird die Spannung am kapazitiven Widerstand nach unten abgetragen. Für die Gesamtspannung U erhält man damit aus dem Zeigerdiagramm:

U = U R 2 + ( U L − U C ) 2 U R Spannung am ohmschen Widerstand U L Spannung am induktiven Widerstand U C Spanung am kapazitiven Widerstand

Aus dieser Gleichung ergibt sich:

  •  
Die Gesamtspannung U erreicht ein Maximum, wenn die Teilspannungen am induktiven und kapazitiven Widerstand gleich groß sind. Sie ist dann gleich der Spannung am ohmschen Widerstand.
  •  
Die Teilspannungen an den einzelnen Widerständen können wesentlich größer als die Gesamtspannung sein.

Aus der genannten Gleichung ergibt sich der Scheinwiderstand (Gesamtwiderstand) Z als Quotient aus Spannung und Stromstärke:

Z = U I = U R 2 + ( U L − U C ) 2 I

Setzt man für die jeweilige Spannung das Produkt aus Stromstärke und Widerstand ein und vereinfacht die Gleichung, so erhält man:

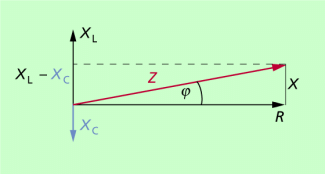
Z = R 2 + ( X L − X C ) 2 Mit X L = ω ⋅ L und X C = 1 ω ⋅ C lautet die Gleichung für den Scheinwiderstand: Z = R 2 + ( ω ⋅ L − 1 ω ⋅ C ) 2 Setzt man X L − X C = X , so erhält man: Z = R 2 + X 2

Diese Beziehungen ergeben sich auch unmittelbar aus dem Zeigerdiagramm für die Widerstände (Bild 3).

Aus den Gleichungen ergibt sich auch:

  •  
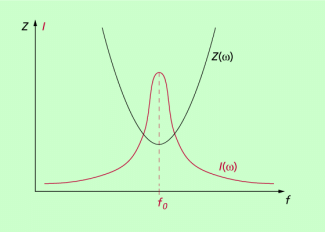
Der Scheinwiderstand erreicht ein Minimum, wenn induktiver und kapazitiver Widerstand gleich groß sind. Die Stromstärke ist in diesem Fall maximal (Bild 4).
  •  
Bei gegebener Induktivität und Kapazität ist der Scheinwiderstand und damit auch die Stromstärke frequenzabhängig, denn für die Kreisfrequenz ω gilt: ω = 2 π ⋅ f .

Der frequenzabhängige Verlauf von Gesamtwiderstand und Stromstärke ist in Bild 4 dargestellt. Er ist folgendermaßen zu erklären: Bei sehr kleiner Frequenz dominiert der kapazitive Widerstand, der Gesamtwiderstand ist relativ groß, die Stromstärke klein. Mit Vergrößerung der Frequenz verkleinert sich der Gesamtwiderstand. Entsprechend vergrößert sich die Stromstärke. Das Minimum des Widerstandes und damit das Maximum der Stromstärke wird unter folgender Bedingung erreicht:

ω ⋅ L = 1 ω ⋅ C Mit ω = 2 π ⋅ f erhält man: 2 π ⋅ f ⋅ L = 1 2 π ⋅ f ⋅ C Die Umstellung der Gleichung nach f ergibt: f = 1 2 π ⋅ L ⋅ C oder mit f = 1 T : T = 2 π ⋅ L ⋅ C

Der letzte Ausdruck ist nicht anderes als die thomsonsche Schwingungsgleichung . Im Resonanzfall sind die Teilspannungen an den Blindwiderständen größer als die Gesamtspannung. Man spricht von Reihenresonanz oder Spannungsresonanz. Da der Scheinwiderstand im Resonanzfall ein Minimum hat (Z = R), verwendet man diew Reihenschaltung auch als Siebkreis oder Siebkette.
Bei weiterer Vergrößerung der Frequenz dominiert der induktive Widerstand. Der Gesamtwiderstand vergrößert sich wieder, die Stromstärke verringert sich.

Aus dem Zeigerdiagramm der Widerstände (Bild 3) ergibt sich auch unmittelbar die Phasenverschiebung ϕ zwischen Stromstärke und Spannung:

tan   ϕ = X L − X C R = ω ⋅ L − 1 ω ⋅ C R

Je nachdem, ob der induktive Widerstand kleiner oder größer als der kapazitive ist, eilt die Spannung der Stromstärke voraus oder bleibt hinter ihr zurück. Das liefert unterschiedliche Vorzeichen für die Phasenverschiebung.

Berechnung Kapazität reine Widerstände ohmscher Widerstand Scheinwiderstand Siebkreis Induktivität Zeigerdiagramm kapazitiver Widerstand Reihenresonanz Resonanzfall Wirkwiderstand Teilspannungen Wechselstromkreis Siebkette Thomsonsche Schwingungsgleichung Gleichstromkreis Gesamtwiderstand induktiver Widerstand Spannungsresonanz Rechenbeispiel Phasenverschiebung Gesamtspannung Blindwiderstand Reihenschaltung von Wechselstromwiderständen
Lexikon Share
Physik Note verbessern?
 

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

  • 40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
  • Hausaufgabenhilfe per WhatsApp
  • Original Klassenarbeiten mit Lösungen
  • Deine eigene Lern-Statistik
  • Kostenfreie Basismitgliedschaft
Physik kostenlos lernen
Verwandte Artikel
Angaben zum Lexikon
Impressum
© Duden Learnattack GmbH, 2024

Einloggen