Wechselspannung und Wechselstrom

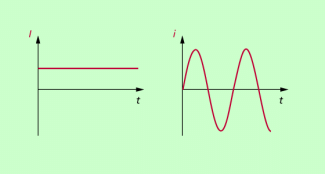
Während bei einer Gleichspannung immer die gleiche Polarität und damit bei einem Gleichstrom die gleiche Flussrichtung vorliegt, wird eine Spannung, deren Polarität sich periodisch ändert, als Wechselspannung bezeichnet. Entsprechend ändert sich die Flussrichtung des Wechselstromes periodisch. Spannung und Stromstärke müssen nicht unbedingt den zeitlichen Verlauf einer Sinusfunktion besitzen. Allerdings ist sinusförmige Wechselstrom technisch am weitesten verbreitet, da er bei der Stromgewinnung in Wechselstromgeneratoren entsteht. Er lässt sich auch mathematisch relativ einfach beschreiben.
Bei Wechselspannungen bzw. Wechselströmen gibt man in der Regel die Effektivwerte für Spannung und Stromstärke an. Sie unterscheiden sich von den mittleren Werten und von den Maximalwerten.

Elektromotor und Generator

#Induktion #Lorentzkraft #Bewegte Ladung #Induktionsspannung

Elektrische Spannung

#Spannung #Stromstärke #Volt #Ampere #kirchoffsche Regeln #Widerstand #Gesamtspannung #Gesamtstromstärke

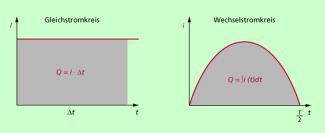
Gleichstrom und Wechselstrom

sodass man definieren kann:

Strom, der seine Flussrichtung periodisch ändert, wird als Wechselstrom bezeichnet.

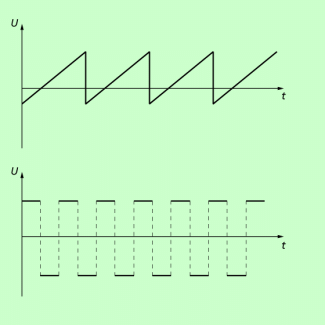
In der Technik spielen auch nichtsinusförmige Verläufe (Bild 2) eine wichtige Rolle, z.B. der sägezahnfömige Verlauf (wird bei Oszillografen zur horizontalen Ablenkung genutzt) oder rechteckige Verläufe, die insbesondere in der Digitaltechnik verwendet werden, da mit ihnen zwei Zustände (ein - aus, high - low) dargestellt werden können.
Wir beschränken uns nachfolgend auf die genauere Kennzeichnung von sinusförmigem Wechselstrom.

Sinusförmiger Wechselstrom

Sinusförmiger Wechselstrom kann als harmonische Schwingung aufgefasst werden. Man kann ihn damit mit den gleichen Größen wie andere harmonische Schwingungen beschreiben. Die sich periodisch ändernden Größen sind die Spannung und die Stromstärke.
Der Verlauf von Spannung und Stromstärke erfolgt nach der Sinus- oder Kosinusfunktion und kann mit folgenden Gleichungen beschrieben werden:

$\begin{array}{l} u = u_{\max} . \sin ω t \\ i = i_{\max} . \sin ω t \\ u_{\max} Maximalwert der Wechselspannung \\ i_{\max} Maximalwert der Wechselstromstärke \\ ω Kreisfrequenz \end{array}$

Die Kreisfrequenz $ω$ hängt unmittelbar mit der Frequenz zusammen. Es gilt:
$\begin{array}{l} ω = 2 π \cdot f = \frac{2 π}{T} \\ f Frequenz des Wechselstromes \\ T Schwingungsdauer \end{array}$
Für Netzwechselstrom beträgt die Frequenz 50 Hz und damit die Schwingungsdauer 0,02 s. Das in den Gleichungen stehende Produkt aus Kreisfrequenz und Zeit ergibt einen Winkel in Bogenmaß. Es gilt also:
$ω t = 2 π \cdot f \cdot t = ϕ$
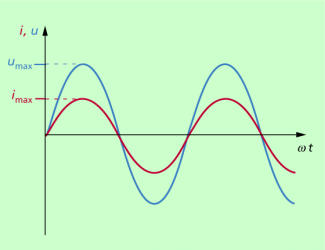
Das ist bei der Darstellung von Wechselspannung und Wechselstromstärke in Diagrammen von Bedeutung. So ist es üblich, die Spannung bzw. die Stromstärke gegen den Winkel in Bogen- oder Gradmaß oder gegen die Zeit aufzutragen. In Bild 3 ist der Winkel gewählt.

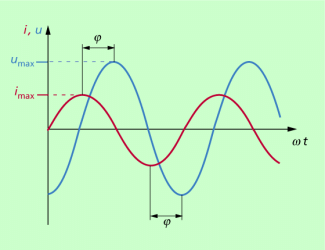
Spannung und Stromstärke können die gleiche Phase haben, d.h. zu den gleichen Zeiten Maxima oder Minima erreichen, so wie das in Bild 3 dargestellt ist. Befinden sich induktive oder kapazitive Widerstände im Wechselstromkreis, so tritt zwischen Spannung und Stromstärke eine Phasenverschiebung auf, die manchmal als $Δ ϕ$ und manchmal einfach als $ϕ$ bezeichnet wird. Für den in Bild 4 dargestellten Fall, dass die Spannung später das Maximum erreicht als die Stromstärke, würden die Gleichungen für Wechselstromstärke und Wechselspannung lauten:
$\begin{array}{l} i = i_{\max} \cdot \sin ω t und u = u_{\max} \cdot \sin (ω t - ϕ) \\ Zum Zeitpunkt t = 0 wäre dann: \\ u = u_{\max} \cdot \sin (- ϕ) \\ u = - u_{\max} \cdot \sin ϕ \\ Bei 0 > ϕ > \frac{π}{2} wäre damit u negativ . \end{array}$

Mittelwerte von Stromstärke und Spannung

Stromstärke und Spannung schwanken ständig zwischen den positiven und dem negativen Maximalwert, den wir als
$\begin{array}{l} i_{\max} bzw . als u_{\max} bezeichnen, für die aber auch die \\ Bezeichnungen \hat{i} oder \hat{u} üblich sind . \end{array}$
Die mittlere Stromstärke entspricht im i-t-Diagramm der Fläche unter dem Graphen (Bild 5). Diese Fläche ergibt sich für Wechselstrom durch Integration:
$\begin{array}{l} Q = \int_{0}^{T / 2} i_{\max} \cdot \sin ω t d t \\ Mit \int \sin ω t d t = - \frac{1}{ω} \cdot \cos ω t erhält man \\ Q = {[- \frac{i_{\max}}{ω} \cdot \cos ω t]}_{0}^{T / 2} \\ Mit ω = \frac{2 π}{T} und Einsetzen der Grenzen ergibt sich: \\ Q = - \frac{i_{\max}}{ω} \cdot \cos \frac{2 π}{T} \cdot \frac{T}{2} - \frac{i_{\max}}{ω} \cdot \cos 0 \\ Q = - \frac{i_{\max}}{ω} \cdot \cos π - (- \frac{i_{\max}}{ω} \cdot \cos 0) \\ Mit \cos π = - 1 und \cos 0 = 1 erhält man: \\ Q = \frac{2 i_{\max}}{ω} \\ Wendet man die Beziehung I = \frac{Q}{t} für eine Halbschwingung \\ an, so erhält man: \\ \bar{i} = \frac{Q}{T / 2} = \frac{2 i_{\max} \cdot 2}{ω \cdot T} = \frac{4 i_{\max} \cdot T}{2 π \cdot T} \\ \bar{i} = \frac{2 i_{\max}}{π} \approx 0,64 i_{\max} \\ Entsprechend ergibt sich für den Mittelwert der Spannung: \\ \bar{u} = \frac{2 u_{\max}}{π} \approx 0,64 u_{\max} \end{array}$

Die angegebene mittlere Stromstärke entspricht der Stromstärke von gleichgerichtetem Wechselstrom. Man bezeichnet den Mittelwert daher auch als Gleichrichtwert.

Effektivwerte von Stromstärke und Spannung

Für die Praxis von größerem Interesse sind die sogenannten Effektivwerte. Es sind diejenigen Werte für Stromstärke und Spannung im Wechselstromkreis, bei denen die gleiche Leistungsabgabe erfolgt wie bei eben diesen Werten im Gleichstromkreis.
Der Effektivwert eines sinusförmigen Größe y ist allgemein definiert als:

$\begin{array}{l} y_{e f f} = \sqrt{\frac{1}{T} \cdot \int_{t}^{t + T} y^{2} (t) d t} \\ Mit y = y_{\max} \cdot \sin ω t erhält man: \\ y_{e f f} = \sqrt{\frac{1}{T} y_{\max}^{2} \cdot \int_{t}^{t + T} \sin^{2} ω t d t} = \sqrt{\frac{1}{T} y_{\max}^{2} \cdot \frac{T}{2}} \\ y_{e f f} = \frac{y_{\max}}{\sqrt{2}} \end{array}$

Damit erhält man für die Effektivwerte von Wechselstromstärke und Wechselspannung die Gleichungen:

$\begin{array}{l} i_{e f f} = I = \frac{i_{\max}}{\sqrt{2}} \approx 0,7 i_{\max} \\ u_{e f f} = U = \frac{u_{\max}}{\sqrt{2}} \approx 0,7 u_{\max} \end{array}$

Physikalisch ergibt sich der Effektivwert von Stromstärke und Spannung auch durch die folgende Überlegung: Die momentane Leistung an einem ohmschen Widerstand im Wechselstromkreis ergibt sich als:
$P = u \cdot i = u_{\max} \cdot i_{\max} \cdot \sin^{2} ω t$
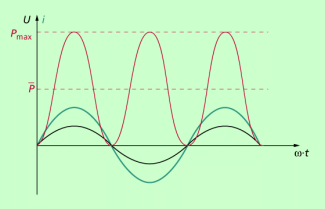
Nun interessiert in der Regel nicht die momentane Leistungsabgabe, sondern der ihr zeitlicher Mittelwert. Dieser mittlere Wert beträgt, wie aus Bild 6 erkennbar ist,
$\bar{P} = \frac{1}{2} i_{\max} \cdot u_{\max} oder \bar{P} = \frac{i_{\max}}{\sqrt{2}} \cdot \frac{u_{\max}}{\sqrt{2}}$

Dieser Mittelwert der Leistung ist gleich der tatsächlich abgegebenen Leistung. Aus der Gleichung lassen sich direkt die Effektivwerte ablesen.

Der Effektivwert der Spannung betrug bis 1989 in Deutschland und vielen anderen Ländern 220 V. Danach erfolgt die allmähliche Umstellung auf 230 V. Bis zum Jahre 2003 gilt dafür eine Spannungsdifferenz von + 6% (243 V) bis - 10% (207 V). Grundlage dafür ist die DIN IEC 38. Nach 2003 soll die Spannungsdifferenz endgültig festgelegt werden.

Lernprobleme in Physik?

Mit deinem persönlichen Nachhilfe-Tutor Kim & Duden Learnattack checkst du alles. Jetzt 30 Tage risikofrei testen.

KI-Tutor Kim hilft bei allen schulischen Problemen
Individuelle, kindgerechte Förderung in Dialogform
Lernplattform für 9 Fächer ab der 4. Klasse
Über 40.000 Erklärvideos, Übungen & Klassenarbeiten
Rund um die Uhr für dich da

Jetzt in Physik durchstarten

Angaben zum Lexikon

Impressum