Trägheitsmomente

Bei einer geradlinigen Bewegung hängt die Änderung des Bewegungszustandes eines Körpers von der wirkenden Kraft und von der Masse des Körpers ab. Die analogen Größen bei der Rotation sind das Drehmoment und das Trägheitsmoment.

Das Trägheitsmoment gibt an, wie träge ein drehbar gelagerter Körper gegenüber der Änderung seines Bewegungszustandes ist.

Formelzeichen: J
Einheit: ein Kilogramm mal Quadratmeter $(1\text{kg}\cdot {\text{m}}^2)$

Berechnung von Trägheitsmomenten

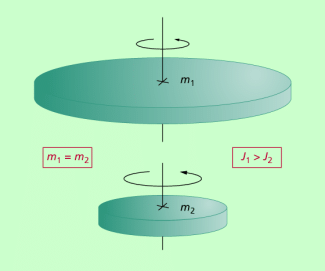
Das Trägheitsmoment eines beliebigen Körpers ist von seiner Masse und der Masseverteilung bezüglich der Drehachse abhängig (Bild 1). Wir betrachten nachfolgend nur die Trägheitsmomente von Körpern, bei denen die Drehachse durch den Schwerpunkt (Massemittelpunkt) verläuft. Allgemein gilt für das Trägheitsmoment eines beliebigen Körpers:

$\begin{array}{l}J={\displaystyle \sum _{i=1}^n{m}_i\cdot r_i^2\text{ (1) oder in integraler Form }}\\ J={\displaystyle \int r^2\text{d}m}\text{ (2)}\\ m_{\text{i}},\text{d}m\text{ Masseelemente}\\ r_{\text{i}},r\text{ Abstände von der Drehachse}\end{array}$

Trägheitsmoment eines Massepunktes

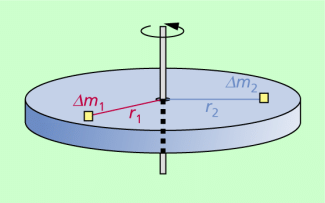
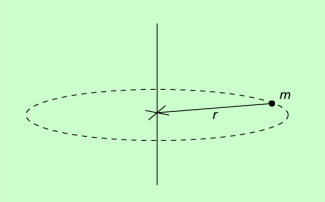
Einem um eine Achse umlaufenden Massepunkt kann ebenfalls ein Trägheitsmoment zugeordnet werden (Bild 3). Wendet man Gleichung (1) darauf an, so ergibt sich:

$\begin{array}{l}\text{Mit }\Delta m_{\text{1}}=m\text{ und }{r}_1=r\text{ erhält man für das Trägheitsmoment }\\ \text{eines Massepunktes:}\\ J=m\cdot r^2\end{array}$

Für einen dünnen Kreisring kommt man zum gleichen Ergebnis.

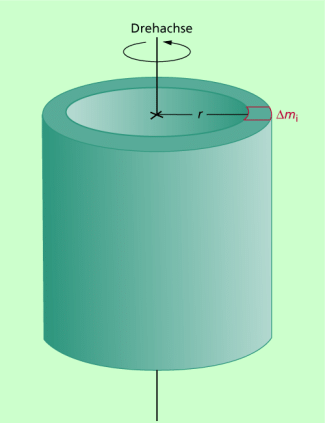
Trägheitsmoment eines dünnen Hohlzylinders um die Längsachse

Ein Hohlzylinder der Gesamtmasse m rotiere um seine Längsachse. Ist die Zylinderwand im Vergleich zum Radius r sehr dünn, so trägt jedes kleine Masseelement
$\Delta m_i\text{ mit }{J}_i=\Delta m_i\cdot r^2$
zum gesamten Trägheitsmoment J bei. Dieses ergibt sich dann durch Summation:

$\begin{array}{l}J={\displaystyle \sum _{i=1}^n{J}_i=}{\displaystyle \sum _{i=1}^n{m}_i\cdot r^2}\\ \text{Die Summe aller Masseelemente ist gleich der Masse m}\text{.}\\ \text{Folglich ergibt sich für das Trägheitsmoment:}\\ J=m\cdot r^2\end{array}$

Trägheitsmoment eines Vollzylinders um die Längsachse

Im Falle eines Vollzylinders ist keine einfache Summation möglich, sondern das Trägheitsmoment erhält man durch Integration. Die Herangehensweise ist dabei in allen Fällen ähnlich:
Ausgangspunkt ist die allgemeine Gleichung:
$J={\displaystyle \int r^2\text{d}m}$
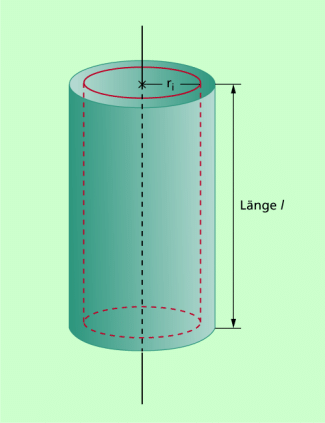
Nun überlegt man sich, wie man am günstigsten das Masseelement dm ausdrücken kann. Ein solches Masseelement wäre z.B. die Masse eines dünnen Kreisringes (in der Skizze rot gezeichnet) mit
$\text{dem Umfang 2}\pi \cdot r,\text{ der Dicke d}r\text{ und der Länge }l\text{.}$
Seine Masse ergibt sich als Produkt aus der Dichte des Stoffes und dem Volumen. Also würde man für das Masseelement erhalten:
$\begin{array}{l}\text{d}m=\rho \cdot dV\\ \text{d}m=\rho \cdot 2\pi \cdot r\cdot \text{d}r\cdot l\\ \end{array}$
Setzt man das in die Gleichung für das Trägheitsmoment ein, so erhält man:

$\begin{array}{l}J=2\pi \cdot l\cdot \rho {\displaystyle \underset{0}{\overset{r}{\int }}{r}^3\text{d}r}\\ J=2\pi \cdot l\cdot \rho \cdot {\left[\frac{r^4}{4}\right]}_0^r\\ J=\frac{\pi }{2}\cdot l\cdot \rho \cdot r^4\\ \text{Nun ist }\pi \cdot r^2\cdot l\text{ das Volumen des Zylinders und }\\ \rho \cdot \pi \cdot r^2\cdot l\text{ seine Masse }m\text{.}\text{ Demzufolge kann man schreiben:}\\ J=\frac{1}{2}m\cdot r^2\end{array}$

Hauptträgheitsachsen und Hauptträgheitsmomente

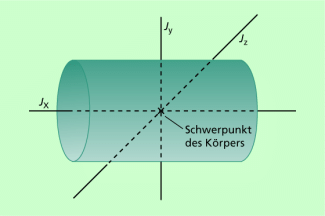
Bei den durch den Schwerpunkt eines Körpers verlaufenden Drehachsen bezeichnet man die in den drei Raumrichtungen x, y und z verlaufenden Achsen als Hauptträgheitsachsen, die betreffenden Trägheitsmomente als Hauptträgheitsmomente (Bild 6). Dabei hat stets eines dieser drei Trägheitsmomente den größten und eines den kleinsten Wert (Ausnahme: die Kugel). Das spielt nicht nur für die Masseanordnung bei Wellen oder Schwungrädern eine Rolle, sondern muss auch bei Kreisel n und ihren Anwendungen beachtet werden.

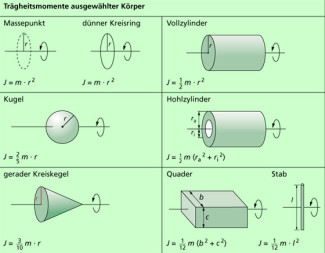
In Bild 7 ist ein Überblick über die Trägheitsmomente unterschiedlicher Körper gegeben. Genannt sind häufig auftretende Fälle. Dabei ist immer zu beachten, dass sich ein bestimmtes Trägheitsmoment immer nur auf eine bestimmte Drehachse bezieht und dass sich mit dem Wechsel der Drehachse auch das Trägheitsmoment ändert.

Der Satz von STEINER

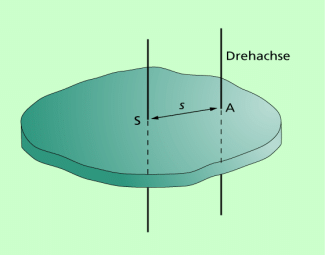
Alle bisherigen Betrachtungen bezogen sich auf Drehachsen, die durch den Schwerpunkt des betreffenden Körpers verlaufen. Es sind natürlich auch andere Drehachsen möglich. Bild 8 zeigt dafür ein Beispiel: Dort verläuft eine Drehachse durch den Punkt A. In diesem Fall kann das Trägheitsmoment nach dem Satz von STEINER berechnet werden. Dieses nach dem schweizer Mathematiker JAKOB STEINER (1796-1863) benannte Gesetz lautet:

$\begin{array}{l}{J}_A=J_S+m\cdot s^2\\ J_A\text{ Trägheitsmoment um die Achse durch A}\\ J_S\text{ Trägheitsmoment um die dazu parallele Achse}\\ \text{ durch den Schwerpunkt S}\\ m\text{ Masse des Körpers}\\ s\text{ Abstand zwischen den beiden Achsen}\end{array}$

Experimentelle Bestimmung von Trägheitsmomenten

Für die experimentelle Bestimmung von Trägheitsmomenten gibt es unterschiedliche Möglichkeiten. Nachfolgend sind zwei dieser Möglichkeiten dargestellt.

Nutzung von Drehschwingungen: Man kann dabei einen Körper an einem Torsionsdraht aufhängen oder auf einem drehbaren, mit einer Spiralfeder verbundenen Tisch lagern (Bild 9a). Für die Schwingungsdauer eines solchen Drehpendels gilt:

$T=2\pi \sqrt{\frac{J}{D}}\text{und damit}J=\frac{T^2}{4{\pi }^2}D$

Zu bestimmen sind also die Schwingungsdauer T und das Direktionsmoment D. Das Direktionsmoment kann über den Zusammenhang
$M=D\cdot \varphi$
ermittelt werden.

Ermittlung mithilfe einer gleichmäßig beschleunigten Drehbewegung:

Es wird eine Experimentieranordnung entsprechend Bild 9b genutzt. Dann kann man das Trägheitsmoment berechnen mit der Gleichung:
$J=m\cdot r^2\left(\frac{g\cdot t^2}{2s}-1\right)$
Diese Gleichung kann in verschiedener Weise hergeleitet werden. Nachfolgend sind zwei verschiedene Möglichkeiten angegeben.

a) Aus dem Energieerhaltungssatz folgt:

$\begin{array}{l}m\cdot g\cdot s=\frac{m}{2}{v}^2+\frac{J}{2}{\omega }^2\\ \text{Mit}\omega =\frac{v}{r}\text{und }v=\frac{2s}{t}\text{erhält man:}\\ m\cdot g\cdot s=\frac{m}{2}\cdot \frac{4s^2}{t^2}+\frac{J}{2}\cdot \frac{4s^2}{t^2\cdot r^2}\\ \text{Die Umstellung nach }J\text{ergibt:}\\ J=\frac{m\cdot r^2\cdot g\cdot t^2}{2s}-m\cdot r^2\text{oder}\\ J=m\cdot r^2\left(\frac{g\cdot t^2}{2s}-1\right)\end{array}$

b) Aus dem Grundgesetz der Dynamik für die Rotation

$\begin{array}{l}M=J\cdot \alpha \text{erhält man}\\ J=\frac{M}{\alpha }\\ \text{Für das Drehmoment gilt: }M=F\cdot r=m(g-a)r\\ \text{Für die Winkelbeschleunigung gilt:}\\ \alpha =\frac{a}{r}\text{und mit }a=\frac{2s}{t^2}\text{erhält man }\alpha =\frac{2s}{r\cdot t^2}\\ \text{Damit folgt für das Trägheitsmoment:}\\ J=\frac{m\cdot g\cdot r-m\cdot a\cdot r}{\frac{2s}{r\cdot t^2}}\\ \text{Wird für}a=\frac{2s}{t^2}\text{gesetzt und die Gleichung umgeformt}\text{,}\\ \text{so erhält man:}\\ J=m\cdot r^2\left(\frac{g\cdot t^2}{2s}-1\right)\end{array}$