Beschleunigung-Zeit-Diagramme
In einem Beschleunigung-Zeit-Diagramm ist für die Bewegung eines Körpers der Zusammenhang zwischen seiner Beschleunigung a und der Zeit t dargestellt. Ein a-t-Diagramm für eine Bewegung mit konstantem Betrag der Geschwindigkeit (gleichförmige geradlinige Bewegung, gleichförmige Kreisbewegung) unterscheidet sich deutlich von einem a-t-Diagramm für eine Bewegung mit konstantem Betrag der Beschleunigung (gleichmäßig beschleunigte geradlinige Bewegung, freier Fall).
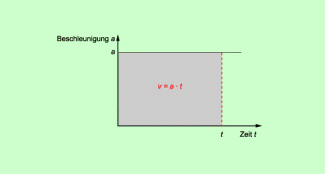
Im a-t-Diagramm hat die Fläche unter dem Graphen eine physikalische Bedeutung. Sie ist gleich der Geschwindigkeit.
In einem Beschleunigung-Zeit-Diagramm ist für die Bewegung eines Körpers der Zusammenhang zwischen seiner Beschleunigung a und der Zeit t dargestellt. Man bezeichnet solche Diagramme auch als a-t-Diagramme, Beschleunigung-Zeit-Diagramme oder t-a-Diagramme.
Bewegungen mit konstantem Betrag der Geschwindigkeit
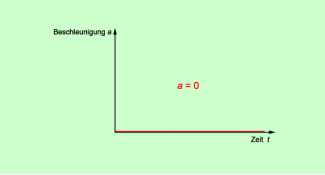
Solche Bewegungen mit einem konstanten Betrag der Geschwindigkeit sind die gleichförmige geradlinige Bewegung und die gleichförmige Kreisbewegung. Bei ihnen bleibt die Geschwindigkeit immer gleich. Die Beschleunigung ist null. Es gilt:
v = konstant, a = 0
Damit ergibt sich als Graph eine Gerade, die mit der t-Achse zusammenfällt (Bild 1).
-
a-t-Diagramm für Bewegungen mit konstantem Betrag der Beschleunigung
Bewegungen mit konstantem Betrag der Beschleunigung längs der Bahn
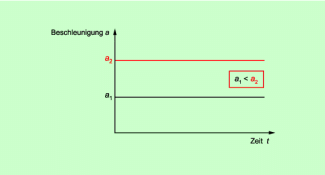
Solche Bewegungen, bei denen die Beschleunigung längs der Bahn einen konstanten Betrag hat, sind die gleichmäßig beschleunigte geradlinige Bewegung, die gleichmäßig beschleunigte Kreisbewegung und der freie Fall als eine spezielle gleichmäßig beschleunigte geradlinige Bewegung. Es gilt:
a = konstant
Der Graph ist eine Gerade, die parallel zur t-Achse verläuft. Je größer die Beschleunigung ist, umso höher liegt der Graph (Bild 2).
-
a-t-Diagramm für Bewegungen mit konstantem Betrag der Beschleunigung
In einem solchen a-t-Diagramm ist die Fläche unter dem Graphen gleich der Geschwindigkeit (Bild 3).
-
Die Fläche unter dem Graphen ist gleich der Geschwindigkeit.