Vektorielle Größen
In der Physik unterscheidet man Größen, die von ihrer Richtung abhängig sind, von richtungsunabhängigen Größen. Solche Größen, bei denen die messbare Eigenschaft sowohl durch einen Betrag als auch durch eine Richtung gekennzeichnet ist, nennt man gerichtete oder vektorielle Größen. Beispiele für solche vektoriellen Größen sind Kraft, Geschwindigkeit oder Beschleunigung.
Im Unterschied dazu gibt es auch ungerichtete Größen wie z. B. den Druck oder die Masse.
In der Physik unterscheidet man Größen, die von ihrer Richtung abhängig sind, von richtungsunabhängigen Größen. Solche Größen, bei denen die messbare Eigenschaft sowohl durch einen Betrag als auch durch eine Richtung gekennzeichnet ist, nennt man gerichtete oder vektorielle Größen. Beispiele für solche vektoriellen Größen sind Kraft, Weg, Geschwindigkeit oder Beschleunigung.
Im Unterschied dazu gibt es auch ungerichtete oder skalare Größen wie z. B. den Druck oder die Masse.
Gerichtete oder vektorielle Größen werden mit einem Pfeil über dem Formelzeichen gekennzeichnet. Beispiele:
| Kraft | |
| Geschwindigkeit | |
| Beschleunigung |
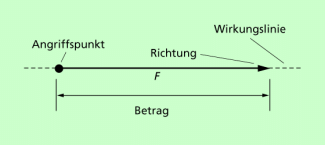
In Skizzen werden sie als Pfeile dargestellt (Bild 2).
-
Kraft als gerichtete Größe
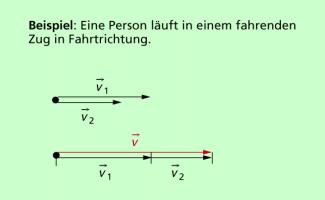
Bei der Addition oder Subtraktion vektorieller Größen ist ihre Richtung zu beachten. Haben zwei vektorielle Größen die gleiche Richtung, so hat auch die resultierende Größe diese Richtung. Die Beträge addieren sich (Bild 3). Haben die beiden Größen die entgegengesetzte Richtung, so subtrahieren sich die Beträge voneinander. Die Richtung der resultierenden Größe hängt davon ab, welche der beiden Größen den größeren Betrag hat.
Sollen dagegen vektorielle Größen addiert werden, die unterschiedliche Richtungen haben, so muss man die Richtungen jeder einzelnen Größe beachten. Die resultierende vektorielle Größe kann man durch geometrische Addition in einer Zeichnung ermitteln.
Fertigt man eine maßstäbliche Zeichnung an, so kann man aus dieser Zeichnung neben der Richtung auch den Betrag der resultierenden Größe ermitteln. Dieses Verfahren nennt man auch Superpositionsprinzip vektorieller Größen.
Den Betrag der resultierenden vektoriellen Größe kann man auch rechnerisch ermitteln. Ein Beispiel ist unter dem Stichwort "Kräftezusammensetzung" zu finden.
Für eine Reihe von Anwendungen genügt es, mit den Beträgen der vektoriellen Größen zu rechnen. Das ist vor allem dann möglich und sinnvoll, wenn man nur mit einer vektoriellen Größe arbeitet oder wenn die Größen gleiche oder entgegengesetzte Richtung haben. Für den Betrag einer Größe schreibt man das Formelzeichen ohne den Pfeil darüber oder man setzt das Formelzeichen mit Pfeil in Betragsstriche:
bedeutet: Die Kraft hat einen Betrag von 12 Newton.
F = 12 N
bedeutet ebenfalls: Die Kraft hat einen Betrag von 12 Newton.
-
Addition gleich gerichteter vektorieller Größen