Exponentieller Zerfall und exponentielles Wachstum

Radioaktiver Zerfall

Beim Zerfall instabiler Atomkerne kann man annehmen, dass die Zahl der je Zeiteinheit zerfallenden Kerne $\Delta N$ proportional zur noch vorhandenen Anzahl N ist:
$\frac{\Delta N}{\Delta t}=-\lambda \cdot N$

Die Zerfallskonstante $\lambda$ ist charakteristisch für den jeweiligen Atomkern, das negative Vorzeichen beschreibt die Tatsache, dass beim Zerfall die Zahl N abnimmt.
Die entsprechende Differenzialgleichung lautet dann
$\frac{\text{d}N}{\text{d}t}=-\lambda \cdot N$.

Die Trennung der Variablen (N und t) und Integration auf beiden Seiten ergibt:
$\frac{\text{d}N}{N}=-\lambda \cdot \text{d}t,also\ln N+C=-\lambda \cdot t$

Mit der Anfangsbedingung, dass $N_0$ die Teilchenzahl zur Zeit $t=0$ ist, erhält man
$C=-\ln N_0$.

Mit $\ln \frac{N}{N_0}=-\lambda \cdot tfo\lg tN=N_0\cdot {\text{e}}^{-\lambda \cdot t}$

Anmerkungen:
(1.) Dem gleichen Gesetz folgen die Anzahl der Zerfälle je Zeiteinheit, d.h. die Zahl der ausgesandten Teilchen, die man messen kann. Aus zwei solchen Intensitätsmessungen lässt sich dann $\lambda$ berechnen:
$\frac{N_1}{N_2}={\text{e}}^{-\lambda \cdot (t_1-t_2)},also\lambda =\frac{1}{t_2-t_1}\cdot \ln \frac{N_1}{N_2}$

Damit kennt man auch die Halbwertzeit $T_H$ des Kernes, die Zeit, in der die Hälfte der anfänglich vorhandenen Kerne zerfallen ist:
$AusN=\frac{1}{2}\cdot N_0=N_0\cdot {\text{e}}^{-\lambda \cdot T_H}fo\lg t\ln 2=\lambda \cdot T_H,also{T}_H=\frac{\ln 2}{\lambda }$

(2.) Das hergeleitete Gesetz gilt nur für eine sehr große Zahl von Teilchen. Einige wenige (oder im Grenzfall ein einzelnes) Teilchen können nicht exponentiell zerfallen. Hier sind nur noch Wahrscheinlichkeitsaussagen über den Zeitpunkt des Zerfalls möglich. Man spricht deshalb von statistischen Gesetzen.

(3.) Viele Zerfalls- und Abbauprozesse in Natur und Technik verlaufen exponentiell. So z.B. auch der Abbau von Alkohol im menschlichen Körper, streng genommen ist er nie zu Ende! Würde man eine Nullpromillegrenze für Blutalkohol im Straßenverkehr ganz streng handhaben und wären die Nachweisgeräte entsprechend empfindlich, dann könnte man dafür bestraft werden, dass man vor einer Woche ein Glas Bier getrunken hat!

Exponentielles Wachstum

Bei Anregungsprozessen in atomaren Systemen kann jedes angeregte Atom $\lambda$ weitere Atome anregen. Die Zahl der angeregten Atome nimmt also im Unterschied zum radioaktiven Zerfall zu gemäß $\frac{\Delta N}{\Delta t}=+\lambda \cdot N.$
Die Lösung entspricht obiger Rechnung und führt zu
$N=N_0\cdot {\text{e}}^{\lambda \cdot t}.$

Diese bedeutsame Gleichung gilt nicht nur für physikalische Systeme, sondern z.B. auch für Ihr Geld auf einem Sparkonto ($\lambda$ ist dann der Zinssatz), für Wirtschaftswachstum, für das Anwachsen von Tierpopulationen und Bakterienstämmen u.a.m. Das stimmt dann und nur dann, wenn $\lambda$ konstant bleibt und wenn keine Störungen auftreten. Das ist in Wirtschaft und Natur selten der Fall. Fast immer sind der Lebensraum, die Nahrungsquellen oder andere Ressourcen begrenzt.

Anmerkung:
Beachten Sie, dass exponentielles Wachstum immer schneller wird! Wann hat sich Ihr Geld nach diesem Gesetz verdoppelt? Es ist ${\text{N = 2N}}_{\text{0}}\text{, also }\lambda \cdot t=\ln 2\approx \mathrm{0,7.}$ Das Produkt aus Zinssatz und Zahl der Jahre ist 0,7; bei einem Zinssatz von $7\%$ (0,07) verdoppelt sich Ihr Geld in 10 Jahren, in 20 Jahren verfügen Sie über den vierfachen Betrag und in 100 Jahren über den $2^{10}=1024fachenBetrag$– wenn nichts dazwischen kommt!

Gebremstes Wachstum

Wir suchen ein mathematisches Modell für den Normalfall von Wachstum in der Natur. Kleine Populationen wachsen so, wie eben beschrieben, bei zu starkem Anwachsen wird der Anstieg wegen begrenzter Ressourcen immer langsamer. Ein brauchbarer Ansatz ist offenbar die folgende Differenzialgleichung:
$\frac{\text{d}N}{\text{d}t}=\lambda \cdot N\cdot (1-N)(N\le 1)$

Für kleine Werte von N ist der Zuwachs proportional N, je näher aber N dem Grenzwert 1 kommt, desto langsamer wächst die Population.
Auch hier lassen sich die Variablen trennen. Die Integration ist etwas aufwendig und soll hier übergangen werden. Es kann leicht nachgeprüft werden, dass folgende Gleichung eine Lösung ist:
$N=\frac{N_0}{N_0+(1-N_0)\cdot {\text{e}}^{-\lambda \cdot t}}(N=N_0\text{für}t=0)$

Offensichtlich strebt N für $t\to \infty$ gegen 1. Das gilt für jeden Startwert.

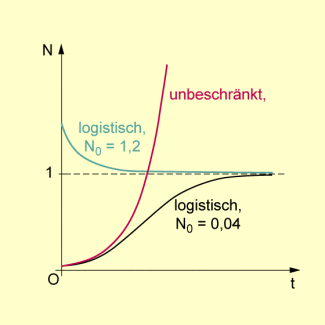
Deterministisches Chaos

Bisher haben wir mit kontinuierlichen Veränderungen gerechnet und uns dabei der Differenzialrechnung bedient. Vorgänge in der Natur sind aber oft sprunghaft. So haben viele Tiere einmal im Jahr Nachwuchs, sodass die Frage nach der Population zwischendurch sinnlos ist. Auch in der Physik, z.B. beim Laser, verlaufen oft die wesentlichen Prozesse quantenhaft.

Wir tragen dem Rechnung, indem wir die Gleichung $\frac{\Delta N}{\Delta t}=\lambda \cdot N\cdot \left(1-N\right)$ nicht mittels $\Delta t\to 0$ in eine Differenzialgleichung umwandeln, sondern wir setzen $\Delta t=1$ und erhalten eine Rekursionsgleichung für die Folge ${\text{N}}_{\text{i}}\text{ :}$ $N_{i+1}=N_i+\Delta N=N_i+\lambda \cdot N_i\cdot \left(1-N_i\right)$

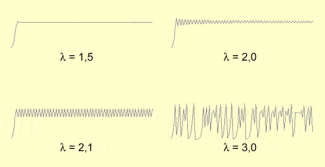
Jeder Wert ergibt sich eindeutig aus dem vorhergehenden. Als Endwert für $N_{i+1}=N_i$ ergibt sich $N_{\infty }=1.$ Wie schnell dieser Wert erreicht wird, hängt von $\lambda$ ab. Wie die Abbildungen zeigen, wird er in manchen Fällen gar nicht erreicht, der Verlauf kann auch chaotisch werden.
Untersuchen Sie selbst das merkwürdige Verhalten dieser Folge! Nehmen Sie die Startwerte 0,04 und 1,2 und für $\lambda$ die Werte 1,5; 2; 2,1; ...; 3.