Inverse Funktion (Umkehrfunktion)
Eine Funktion heißt umkehrbar eindeutige (eineindeutige) Funktion, wenn nicht nur jedem Argument eindeutig ein Funktionswert zugeordnet ist, sondern auch umgekehrt zu jedem Funktionswert genau ein Argument gehört.
Kauft man bei einem Bäcker Brötchen einer bestimmten Sorte, so wird der zu zahlende Preis eindeutig von der Anzahl der gekauften Brötchen bestimmt. Würfelt jeder Schüler einer Gruppe genau einmal mit einem normalen Spielwürfel, so kann jedem Schüler auf diese Weise eindeutig die gewürfelte Augenzahl zugeordnet werden: In beiden Fällen handelt es also um eindeutige Zuordnungen – die Vorschriften beschreiben Funktionen.
![]()
Trotzdem besteht zwischen den beiden beschriebenen Sachverhalten aus mathematischer Sicht ein wesentlicher Unterschied: Während im ersten Fall zu jeder Preisangabe auch eindeutig eine bestimmte Brötchenanzahl gehört (eben genau die Anzahl der Brötchen, die man für das Geld erhält), ist die Zuordnung „geworfene Augenzahl Schüler“ nicht eindeutig, da mehrere Schüler die gleiche Augenzahl geworfen haben können (was bei mehr als sechs Spielern ja unumgänglich ist).
Allgemein formuliert: Im ersten Fall ist die Zuordnung in beiden Richtungen, im zweiten Fall nur in der Ausgangsrichtung, aber nicht in der umgekehrten Richtung eindeutig.
Man sagt:
- Eine Zuordnung (Abbildung) heißt umkehrbar eindeutig (eineindeutig), wenn durch sie nicht nur jedem Element des Definitionsbereichs eindeutig ein Element des Wertebereichs zugeordnet wird, sondern auch umgekehrt zu einem Element des Wertebereichs genau ein Element des Definitionsbereichs gehört. In beiden Richtungen stellt die Abbildung also dann eine Funktion dar – die Funktion ist umkehrbar.
Oder anders formuliert:
- Eine Funktion heißt umkehrbar eindeutige (eineindeutige) Funktion, wenn nicht nur jedem Argument eindeutig ein Funktionswert zugeordnet ist, sondern auch umgekehrt zu jedem Funktionswert genau ein Argument gehört.
Beispiel 1:
In diesem Sinne wird also beispielsweise durch die Gleichung eine umkehrbar eindeutige Abbildung (eine umkehrbare Funktion) beschrieben, da durch sie jeder (reellen) Zahl eindeutig eine andere reelle Zahl zugeordnet wird und umgekehrt auch zu jeder Zahl eindeutig eine Zahl gehört.
-
Graph einer linearen Funktion
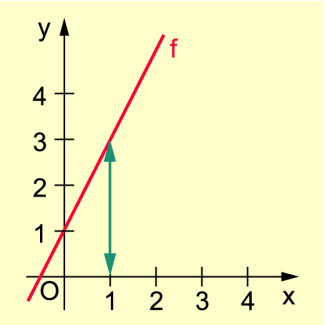
Beispiel 2:
Durch die Gleichung wird eine nicht umkehrbar eindeutige Abbildung (eine nicht umkehrbare Funktion) beschrieben, denn jedem Argument wird zwar genau ein Funktionswert zugeordnet, aber zu jeder Zahl aus dem Wertevorrat (außer ) gehören zwei Argumente.
-
Graph einer quadratischen Funktion (Normalparabel)
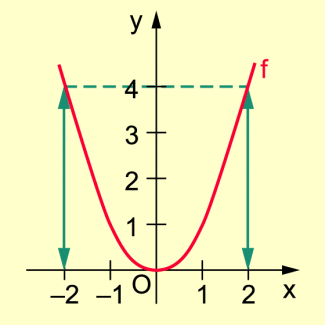
Beispiel 3:
Aus dem Graphen einer Funktion lässt sich gut erkennen, ob diese Funktion umkehrbar ist: Da in diesem Falle zu jedem -Wert nur genau ein -Wert gehört, darf jede Parallele zur -Achse (die ja einen bestimmten -Wert beschreibt) den Graphen der Funktion auch nur (höchstens) einmal schneiden.
-
Graphen einer umkehrbaren und einer nicht umkehrbaren Funktion
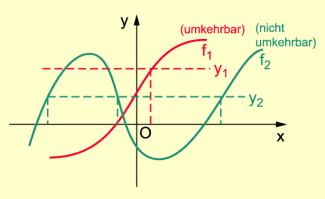
Da bei einer umkehrbaren Funktion die Abbildung „in beiden Richtungen“ eindeutig ist, gilt:
- Durch Vertauschen der Elemente in allen Paaren einer eineindeutigen Funktion entsteht wieder eine Funktion. Man nennt diese Funktion Umkehrfunktion (inverse Funktion) von und bezeichnet sie mit .
Diese Schreibweise hat einen andere Bedeutung als in der Potenzrechnung, wo gilt.
Die Funktionsgleichung der Umkehrfunktion von erhält man, indem man nach auflöst und danach und vertauscht (da es üblich ist, die Elemente des Definitionsbereichs mit und die Elemente des Wertebereichs mit zu bezeichnen).
Beispiel 4:
Die Funktion lässt sich auch durch die Menge von Wertepaaren beschreiben.
-
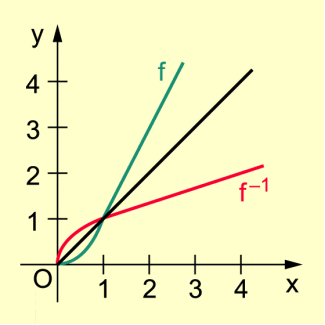
Graphen einer linearen Funktion und ihrer Umkehrfunktion
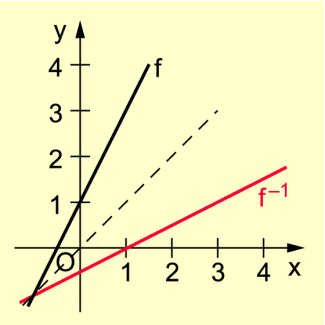
Diese Funktion ist – wie oben gezeigt – umkehrbar. Die Umkehrfunktion wird durch die Menge beschrieben.
Um die Funktionsgleichung zu erhalten, lösen wir nach auf:
Dann vertauschen wir und :
Eine Überprüfung zeigt, dass man mittels dieser Gleichung zu der obigen Paarmenge für gelangt.
Beispiel 5:
Die Funktion ist nicht eineindeutig und daher im Ganzen nicht umkehrbar. Verwendet man aber als Definitionsbereich die Menge der nichtnegativen reellen Zahlen , so erhält man eine eineindeutige Funktion.
Um die Funktionsgleichung von zu erhalten, lösen wir nach auf:
Dann vertauschen wir und :
Zeichnet man jeweils die Graphen von und in ein Koordinatensystem, so ist erkennbar, dass die Graphen der beiden Funktionen achsensymmetrisch zur Winkelhalbierenden des I. und III. Quadranten sind. Diese Eigenschaft besitzen alle Graphen von zueinander inversen Funktionen.
-
Graphen einer quadratischen Funktion und ihrer Umkehrfunktion