Euklid von Alexandria
* etwa 365 v.Chr.
† etwa 300 v.Chr.
EUKLID fasste in den „Elementen“ wesentliche Teile des mathematischen Wissens seiner Zeit zusammen und gründete es auf Axiome und Postulate (Axiomensystem der euklidischen Geometrie). EUKLIDS fünftes Postulat, das sogenannte Parallelenaxiom, spielte in der Geschichte der Mathematik eine besondere Rolle. Der Versuch, dieses Axioms zu beweisen, führte zu einer Gabelung in die euklidische Geometrie einerseits und in nichteuklidische Geometrien andererseits.
Bekannt sind ferner Arbeiten EUKLIDS zur geometrischen Optik.
Zu Leben und Wirken EUKLIDS
Über das Leben EUKLIDS (griechisch: Eukleides) ist so gut wie nichts bekannt. Es scheint lediglich gesichert, dass er eine Zeit lang in Alexandria gelebt und gewirkt hat. Seine Lebensdaten, mit etwa 365 bis etwa 300 v.Chr. angegeben, sind geschätzte Daten und wohl der Einprägsamkeit wegen so gewählt worden.
Das Verdienst EUKLIDS ist es, die Mathematik als Wissenschaft begründet zu haben. Schon vor ihm gab es bedeutende Mathematiker wie beispielsweise THALES, PYTHAGORAS und EUDOXOS, aber die mathematischen Erkenntnisse waren isoliert, es gab keinen Zusammenhang zwischen ihnen, Regeln und Gesetze wurden oft in Form von Handlungsanweisungen angegeben. EUKLID fasste all dieses Wissen in einem System mit streng wissenschaftlichem Aufbau zusammen, in dem jede Erkenntnis auf eine schon vorher gewonnene gesicherte Einsicht zurückgeführt und durch logische Schlussfolgerungen abgesichert wurde (… was zu beweisen war), und andererseits aus diesen Erkenntnissen neue deduktiv abgeleitet wurden. Zum Beispiel wird der Satz über die Winkelsumme eines Vierecks auf den entsprechenden Satz über das Dreieck und dieser wiederum auf Sätze über Wechselwinkel und Stufenwinkel zurückgeführt. So entsteht gleichsam ein Gebäude. Weil irgendwo mit einer nicht mehr rückführbaren Annahme begonnen werden muss, setzte EUKLID an den Anfang (gleichsam als Fundament) eine Reihe von Thesen, die der Anschauung entnommen waren und als einleuchtend zu akzeptieren sind.
Die „Elemente“ (griechisch: stoicheia) als EUKLIDS berühmtestes Buch beginnen daher mit einer Reihe von Definitionen, wie z.B. für die Begriffe Punkt, Strecke, Linie, Kreis, Rechteck, Umfang.
Daran schließen sich fünf sogenannte Postulate an, Forderungen gleichsam, die in diesem System erfüllbar sein sollen. Solche sind etwa Jeden Punkt kann man mit jedem anderen durch eine Strecke verbinden bzw. Jede begrenzte Linie kann man geradlinig verlängern (implizit steckt in diesen Postulaten die Beschränkung auf Zirkel und Lineal bei allen Konstruktionen).
Anschließend werden neun Axiome aufgezählt. Dazu gehören solche wie Was einem Dritten gleich ist, ist auch untereinander gleich; Gleiches zu Gleichem hinzugefügt, ergibt Gleiches; Das Ganze ist größer als sein Teil. Aus all diesen Voraussetzungen soll nun alles Weitere abgeleitet werden.
Das euklidische Parallelenaxiom
Das fünfte Postulat hat in der Geschichte der Mathematik eine besondere Rolle gespielt. Es lautet bei EUKLID:
Wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann treffen sich die zwei geraden Linien bei Verlängerung ins Unendliche auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind.
Man bezeichnete dieses Postulat (die Begriffe Axiom und Postulat wurden nicht scharf getrennt) als „Parallelenaxiom“. Da angestrebt wurde, mit möglichst wenig Voraussetzungen auszukommen, versuchten in der Folge fast alle bedeutenden Mathematiker dieses (auch aus dem Rahmen fallende) Axiom auf andere Axiome zurückzuführen. Das misslang, und es wurden lediglich andere äquivalente Fassungen gefunden.
Schließlich kam man auf den Gedanken, zu untersuchen, was denn folgen würde, wenn man dieses Axiom einfach wegließe. Es zeigte sich, dass in diesem Fall eine „andere“, aber in sich widerspruchsfreie Mathematik entstand.
Ein Beispiel dafür ist die Geometrie auf der Kugeloberfläche. Zwei verschiedene Längenkreise schneiden den Äquator jeweils im rechten Winkel, und dennoch treffen sie sich in den Polen, und das so entstehende „Dreieck“ hat eine Winkelsumme von über 180°. Auf diese Weise entstanden – entwickelt vor allem von CARL FRIEDRICH GAUSS, JANOS BOLYAI und NIKOLAI IWANOWITSCH LOBATSCHEWSKI – sogenannte nichteuklidische Geometrien.
(Seither bezeichnet man die in der Schule gelehrte, in der Ebene gültige Geometrie als euklidische Geometrie).
Zu EUKLIDS „Elementen“
Die „Elemente“ bestehen aus 13 Büchern, von denen der größte Teil erhalten geblieben ist. Einige Inhalte seien hier genannt:
- Vom Punkt zum pythagoreischen Lehrsatz
- Geometrische Algebra
- Kreislehre
- Ein- und umbeschriebene regelmäßige Vielecke
- Proportionen (einschließlich Irrationalitäten)
...
- Teilbarkeit, Primzahlen
- Quadrat- und Kubikzahlen
- Geometrische Reihen
...
- Elementare Stereometrie
- Exhaustionsmethode: Pyramide, Kegel, Kugel
- Reguläre Polyeder
Dank ihrer logischen Struktur wurden die „Elemente“ zum grundlegenden Lehrbuch der Mathematik. Als eines der ersten mathematischen Bücher wurden sie 1482 in Venedig erstmals gedruckt und waren das am häufigsten gedruckte Buch neben der Bibel. Beispielsweise sollen noch im 16. Jahrhundert Kandidaten für den Grad des Magisters an der Pariser Universität verpflichtet gewesen sein, zu beeiden, dass sie Vorlesungen über die ersten sechs Bücher der „Elemente“ gehört hätten. In THEODOR STORMS Novelle „Der Schimmelreiter“ lernt der spätere Deichgraf Hauke Haien als Knabe Mathematik aus einem Buch von EUKLID, das er auf dem Dachboden gefunden hatte.
Es verdient Erwähnung, dass sich in den „Elementen“ keinerlei Anwendungen der Erkenntnisse finden. Für EUKLID war jede Nutzung der Mathematik außer der Schulung des Geistes verpönt. In einer (allerdings auch anderen Mathematikern zugeschriebenen) Anekdote wird berichtet, EUKLID habe einem seiner Jünger, als dieser ihn nach dem Nutzen eines bestimmten Lehrsatzes fragte, Geld überreichen lassen, denn er müsse doch sehr arm sein, wenn er nach dem Nutzen solchen Wissens frage.
Eine andere Anekdote besagt: Als der ägyptische König EUKLID fragte, ob er für ihn nicht einen leichteren Zugang zur Mathematik wisse, antwortete EUKLID, es gäbe keinen „Königsweg“ für die Wissenschaft.
Weitere wissenschaftliche Leistungen EUKLIDs
Den größten Teil der in den „Elementen“ dargelegten Erkenntnisse hat EUKLID von Vorgängern oder Zeitgenossen übernommen. Manches ist sicherlich auch von ihm gefunden, und einiges ist bis heute mit seinem Namen verknüpft.
Im Folgenden seien einige Beispiele dafür angeführt:
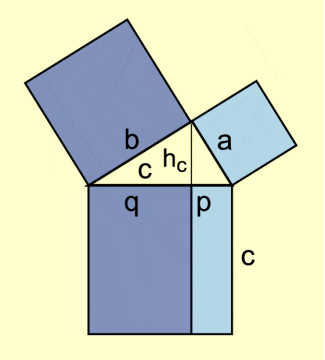
- Satz von EUKLID (auch „Kathetensatz“):
Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächeninhaltsgleich dem Rechteck aus der Hypotenuse und dem zugehörigen Hypotenusenabschnitt (Bild 2): - Euklidischer Beweis zum Satz Es gibt keine größte Primzahl.
Angenommen, es gäbe eine größte Primzahl. Sie sei p. Dann bilde man das Produkt aller Primzahlen und addiere dazu 1. Die so entstandene Zahl ist durch keine der bis dahin bekannten Primzahlen teilbar, denn sie lässt bei Division stets den Rest 1. Also ist sie entweder selbst eine Primzahl (größer als p) oder sie hat Primteiler, die notwendig größer als p sind. Das ist ein Widerspruch zu der Annahme, und diese muss demnach falsch sein. - Euklidischer Algorithmus
Das ist ein Verfahren, um den größten gemeinsamen Teiler zweier Zahlen zu ermitteln. Das Vorgehen sei an einem Beispiel vorgestellt. Es soll der größte gemeinsame Teiler (ggT) von 903 und 645 gefunden werden. Man rechnet:
Der größte gemeinsame Teiler von 903 und 645 ist 129.
(Das Verfahren lässt sich bei einer Verbindung von Division und Subtraktion verkürzen.)
Viele der von EUKLID angeschnittenen Fragen reizten über Jahrhunderte hinweg die Mathematiker zu weiteren Untersuchungen, so z.B. der vollkommenen Zahlen.
Eine Zahl heißt vollkommen, wenn sie gleich der Summe ihrer echten Teiler ist. Eine solche Zahl ist beispielsweise die 6, denn ihre Teiler sind 1, 2 und 3, und es ist .
EUKLID gab bereits vor: Wenn eine Primzahl ist, dann ist eine vollkommene Zahl. Für n = 3 erhält man dabei und 28 als eine vollkommene Zahl. EULER z.B. bewies, dass alle geraden vollkommenen Zahlen diese von EUKLID angegebene Form haben.
EUKLID war auch auf anderen Gebieten wirksam. So veröffentlichte er Werke über Musiktheorie (Sectio canonis), über Perspektive (Optica) und über Astronomie (Phainomena).
-
Figur zur Satzgruppe des Pythagoras