Grenzverhalten von Funktionen

Ein einfaches Beispiel soll dies verdeutlichen:

Mehrere Schafzüchter vereinigen einen Teil ihrer Bestände zu einer gemeinsamen Herde. Der Anteil jedes Züchters an dem durch Verkauf von Milch, Fleisch und Wolle erzielten Erlös möge nach der von ihm eingebrachten Tieranzahl berechnet werden.

Zu einem bestimmten Zeitpunkt umfasst die Herde 500 Tiere. Züchter Adams hat dazu nur 50 Schafe aus seinem sehr großem Bestand beigesteuert. Mit dem ihm am Jahresende korrekt berechneten und ausgezahlten Ertragsanteil ist er nicht recht zufrieden und überlegt, wie sich dieser erhöhen ließe: Verdopple ich meinen Anteil, so verdoppelt sich auch mein Gewinn …

Wir diskutieren diese Überlegung unter der Voraussetzung, dass einer Herdenvergrößerung aufgrund der zur Verfügung stehenden Weidefläche nichts im Wege stehe und

1. dass jeder der beteiligten Züchter sich wie Züchter Adams entscheidet,
2. dass nur Züchter Adams wie beschrieben vorgeht,
3. dass allein Züchter Adams seinen Beitrag um x Tiere erhöht.

Entscheidet sich jeder der beteiligten Züchter wie Adams und verdoppelt seinen Anteil (Fall 1), dann würde die Herde 1000 Tiere umfassen, wobei 100 davon Züchter Adams gehören. Sein Ertragsanteil wie der der restlichen Züchter wäre dann unverändert $\frac{100}{1000}=\frac{1}{10}bzw.\frac{900}{1000}=\frac{9}{10}$.

Verdoppelt nur Züchter Adams die Anzahl der in die Herde eingebrachten Tiere (Fall 2), dann wäre sein Ertragsanteil $\frac{100}{550}=\frac{2}{11}.$ Sein Anteil würde sich also um $\frac{2}{11}-\frac{1}{10}=\frac{9}{110}$ erhöhen. Dieser Wert $\frac{9}{110}$ multipliziert mit dem Gesamtgewinn Jahr2 ($=\frac{1}{10}$  multipliziert mit dem Gesamtgewinn in Jahr 1) führt zu einer Verdopplung des reinen Gewinns.

Erhöht nun Adams seinen Beitrag um x Tiere (Fall 3), so beträgt sein Ertragsanteil $\frac{50+x}{500+x}$ bzw. die Ertragssteigerung $\frac{50+x}{500+x}-\frac{50}{500}$.

Die Steigerung lässt sich demnach als eine Funktion f mit der Anzahl x der zusätzlich eingebrachten Tiere als unabhängige Variable auffassen:
$f(x)=\frac{9x}{10(500+x)}(x\in \mathbb{N})$

Wie würde sich nun aber der Ertragsanteil von Züchter Adams (theoretisch!) entwickeln, wenn eine beliebige Vergrößerung der Herdengröße möglich wäre und er allein noch Tiere zusätzlich einbringt?

Mithilfe des Grenzwertbegriffs kann die abschließende Frage des „Schafherdenproblems“ vollständig bearbeitet werden:

Wenn man annimmt, dass die Herde beliebig vergrößert werden kann, dann ist zur Beantwortung dieser Frage der Grenzwert der Ertragsteigerungsfunktion $f(x)=\frac{9x}{10(500+x)}(x\in \mathbb{N})$für eine beliebig wachsende Anzahl x an (zusätzlichen) Tieren zu ermitteln:
$\underset{x\to \infty }{\lim }\frac{9x}{10(500+x)}=\frac{9}{10}\underset{x\to \infty }{\lim }\frac{x}{500+x}=\frac{9}{10}$

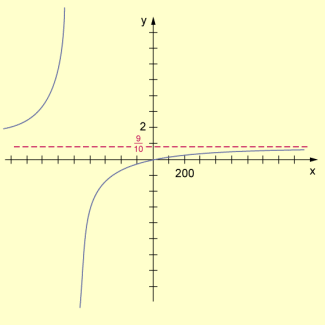
Das heißt: Unter den angegebenen Bedingungen könnte Adams im „theoretischen Grenzfall“ seinen Ertragsanteil um $\frac{9}{10}$ steigern, er erhielte also den gesamten Gewinn – der Anteil der anderen Züchter fiele nicht mehr ins Gewicht.