Materialverflechtungen
Materialflüsse innerhalb einer ökonomischen Einheit drücken technologische und ökonomische Beziehungen zwischen den einzelnen Produktionsebenen aus.
Bei der Planung und Bilanzierung derartiger Wechselbeziehungen wird ein mathematisches Modell mit Matrizen und Vektoren gebildet. Dies ermöglicht es, in komprimierter Form die quantitativen Werte zu erfassen und zu bewerten.
Der hohe Abstraktionsgrad der Darstellung in Matrizenform bedingt stets die sachliche Interpretation der vorliegenden Zahlenwerte. So werden aus der verbalen Beschreibung des Sachverhaltes häufig eine tabellarische Kurzform und eine grafische Darstellung der Beziehungen gewonnen und neben das Matrixmodell gestellt. Dies soll im Folgenden an einem Beispiel demonstriert werden.
Beispiel: In einem Montagebetrieb werden aus fünf verschiedenen Einzelteilen vier Arten von Baugruppen zusammengestellt, die man dann zu den drei Fertigprodukten zusammenfügt.
Die Absatzmengen werden als Zeilenvektoren beschrieben. Als Ersatzteile kommen in den Handel:
- die Fertigprodukte
- die Baugruppen
- die Einzelteile
Den Bedarf an Einzelteilen je Baugruppe bzw. an Baugruppen je Fertigprodukt geben die Tabellen 1 und 2 an; die Beziehungen zwischen den Produktionsebenen sind in der folgenden Abbildung dargestellt.
Wie viele Einzelteile der fünf Sorten müssen von den Zulieferwerken bereitgestellt werden?
Tabelle 1 (Bedarf an Einzelteilen):
| 1 | 2 | 6 | 0 | |
| 4 | 5 | 0 | 2 | |
| 1 | 3 | 5 | 6 | |
| 2 | 1 | 2 | 1 | |
| 0 | 3 | 4 | 3 |
Tabelle 2 (Bedarf an Baugruppen):
| 1 | 0 | 4 | |
| 3 | 1 | 0 | |
| 5 | 3 | 2 | |
| 2 | 2 | 6 |
-
Beziehungen zwischen den Produktionsebene
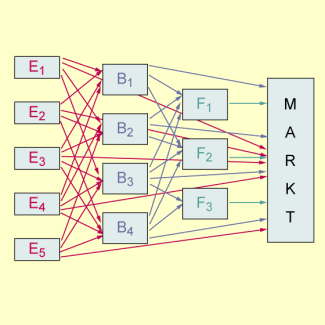
Der Bedarf an Einzelteilen aufgrund der Absatzmenge im Vektor errechnet sich als das Produkt der Matrizen M und N (die sich aus den Tabellen 1 und 2 ergeben) mit dem Vektor wie folgt:
Hinzu kommen die Einzelteile, die für die Ersatzlieferung der Baugruppen erforderlich sind, also
sowie die Einzelteile .
Die Gesamtzahl der erforderlichen Einzelteile liefert dann den Vektor als Summe aus den drei Teilmengen:

