Vektorprodukt zweier Vektoren

Analog zum Skalarprodukt wird ein neues Produkt $\vec{a} \times \vec{b}$ zweier Vektoren $\vec{a} u n d \vec{b}$ definiert. Dazu werden zunächst Anwendungsbeispiele betrachtet.

Beispiel 1: Eine Balkenwaage, an der zwei Gewichtskräfte $\vec{F_{1}} u n d \vec{F_{2}}$ wirken, ist genau dann im Gleichgewicht, wenn $r_{1} \cdot \vec{F_{1}} = r_{2} \cdot \vec{F_{2}}$ ist (Hebelgesetz).

Gleichgewicht an der Balkenwaage (am Hebel)

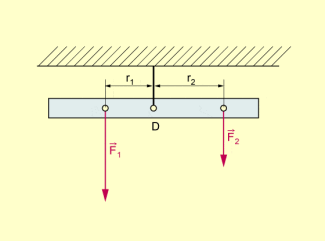
Beispiel 2: Wir betrachten nun im Vergleich dazu eine Scheibe, die im Mittelpunkt D drehbar auf einer Achse gelagert ist und an der ebenfalls zwei Gewichtskräfte $\vec{F_{1}} u n d \vec{F_{2}}$ wirken.

Gewichtskräfte an einer drehbaren Scheibe

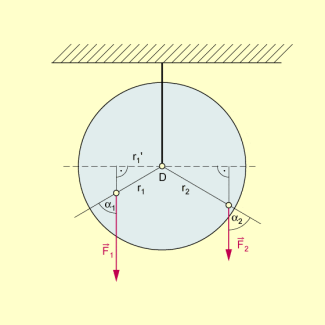
Im Unterschied zur Balkenwaage wirken die Gewichtskräfte $\vec{F_{1}} u n d \vec{F_{2}}$ in diesem Fall nicht senkrecht zum zugehörigen Kraftarm. Die Längen der hier wirksamen Kraftarme lassen sich folgendermaßen berechnen:
$r_{1}' = r_{1} \cdot \sin ϕ_{1} u n d r_{2}' = r_{2} \cdot \sin ϕ_{2}$

Damit herrscht an dieser Scheibe Gleichgewicht, wenn gilt:
$r_{1} \cdot | \vec{F_{1}} | \sin ϕ_{1} = r_{2} \cdot | \vec{F_{2}} | \sin ϕ_{2}$

Bedenkt man, dass auch der Weg – in diesem Fall die Länge des Kraftarms – eine gerichtete Größe ist
$(\vec{r} = \vec{D P})$ ,
so kann man für die beiden Seiten der obigen Gleichung allgemein $| \vec{r} | \cdot | \vec{F} | \cdot \sin ϕ$ schreiben.

Der Ausdruck $| \vec{r} | \cdot | \vec{F} | \cdot \sin ϕ$ beschreibt die Größe des Drehmoments, das an der Scheibe im Punkt D wirkt, wenn die Kraft $\vec{F}$ im Abstand $| \vec{r} |$ vom Drehpunkt D angreift und $\vec{r}$ und $\vec{F}$ den Winkel $ϕ$ einschließen. Darüber hinaus ist die Drehachse der Scheibe senkrecht zu $\vec{r}$ und $\vec{F}$ , d.h. senkrecht zu der Ebene, die durch $\vec{r}$ und $\vec{F}$ gebildet wird.

Definition des Vektorproduktes zweier Vektoren

Orientiert an Ausdrücken der Form $| \vec{r} | \cdot | \vec{F} | \cdot \sin ϕ$ wird nun (analog zum Skalarprodukt) ein neues Produkt $\vec{a} \times \vec{b}$ zweier Vektoren $\vec{a} u n d \vec{b}$ definiert.

Im Unterschied zum Skalarprodukt soll dieses Produkt einen Vektor $\vec{v} = \vec{a} \times \vec{b}$ ergeben. Für diesen Vektor soll außerdem gelten:

$| \vec{v} | = | \vec{a} \times \vec{b} | = | \vec{a} | \cdot | \vec{b} | \cdot \sin ϕ$
$\vec{v}$ ist senkrecht zu der Ebene, die durch $\vec{a} u n d \vec{b}$ gebildet (aufgespannt) wird.
$\vec{v}$ ist so orientiert, dass die drei Vektoren $\vec{a}, \vec{b} u n d \vec{v}$ (in dieser Reihenfolge) ein Rechtssystem bilden.
Das heißt: Dreht man $\vec{a}$ um D auf dem kürzesten Weg in die Richtung von $\vec{b}$ , so bewegt sich eine entsprechend gedrehte Rechtsschraube in die Richtung von $\vec{v}$ .

Vektorprodukt zweier Vektoren (Lage des Produktvektors)

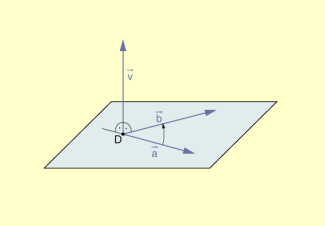
Für das Drehmoment kann man dann $\vec{M} = \vec{r} \times \vec{F}$ schreiben, wobei $| \vec{M} | = | \vec{r} | \cdot | \vec{F} | \cdot \sin ϕ$ die Größe des Drehmoments angibt.
Die Richtung von $\vec{M}$ beschreibt die Richtung der Drehachse, um die ein Körper bei entsprechend einwirkender Kraft gedreht wird.

In der Physik verwendet man das Modell des starren Körpers. Ist ein solcher starrer Körper z.B. im Punkt D mit einem Kugelgelenk drehbar gelagert und greift im Punkt P die Kraft $\vec{F}$ an, dann wirkt in D das Drehmoment $\vec{M} = \vec{r} \times \vec{F}$ auf den starren Körper.

Drehmoment am (Modell des) starren Körper(s)

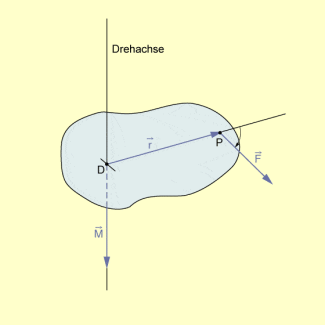
Die Größe dieses Drehmoments ist $| \vec{M} | = | \vec{r} | \cdot | \vec{F} | \cdot \sin ϕ$ .
Darüber hinaus bewirkt die Kraft $\vec{F}$ eine Drehung des Körpers um eine Achse, deren Richtung durch $| \vec{M} | = | \vec{r} | \cdot | \vec{F} | \cdot \sin ϕ$ festgelegt ist.

Fasst man obige Überlegungen verallgemeinert zusammen, so gelangt man zu folgender Definition des Vektorprodukts:

Unter dem Vektorprodukt $\vec{a} \times \vec{b}$ zweier Vektoren $\vec{a} u n d \vec{b}$ versteht man den im Raum durch die folgenden drei Bedingungen charakterisierten Vektor $\vec{v}$ :
$\begin{array}{l} (1) | \vec{v} | = | \vec{a} | \cdot | \vec{b} | \cdot \sin ∢ (\vec{a}; \vec{b}) \\ (2) \vec{v} ⊥ \vec{a} u n d \vec{v} ⊥ \vec{b} \\ (3) S i n d \vec{a} u n d \vec{b} l i n e a r u n a b h ä n g i g, s o b i l \det (\vec{a}; \vec{b}; \vec{v}) e i n Re c h t s s y s t e m . \end{array}$

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Vektorprodukt zweier Vektoren

Definition des Vektorproduktes zweier Vektoren

Rechtliches

Einloggen