Fläche
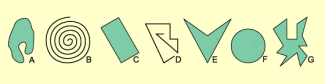
Die Fläche einer ebenen Figur umfasst alle Punkte, die sich im Inneren oder auf dem Rand der Figur befinden.
Zwei Figuren sind flächengleich (die Flächen sind gleich groß, die Figuren haben den gleichen Flächeninhalt), wenn sie so in Teilflächen zerlegt werden können, dass jede der Teilflächen in jeder Figur enthalten ist.
Zum Bestimmen des Flächeninhalts einer Figur kann diese mit Einheitsflächen, zum Beispiel mit Quadraten, ausgelegt werden. Die Maßzahl gibt dann die Anzahl der Einheitsquadrate an, die zum Auslegen der Figur benötigt werden.
Der Flächeninhalt eines Rechtecks kann als Produkt der Seitenlängen berechnet werden.
Fläche ebener Figuren
Jede geschlossene Linie (z. B. Kreislinie, Rechteckslinie ...) zerlegt die Ebene in Teilmengen.
Die Fläche einer ebenen Figur umfasst alle Punkte, die sich im Inneren oder auf dem Rand der Figur befinden. Die Linien A, C, E, F und G erzeugen ebene Figuren. Sie besitzen eine Fläche (Bild 1).
Flächengleichheit – Flächeninhalt
Zwei Figuren sind flächengleich (die Flächen sind gleich groß, die Figuren haben den gleichen Flächeninhalt), wenn sie so in Teilflächen zerlegt werden können, dass jede der Teilflächen in jeder Figur enthalten ist.
-
Linien und Flächen
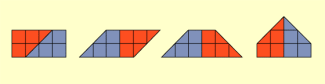
Die Fläche des Rechtecks umfasst acht Kästchen (Bild 2). Das Rechteck kann in das rote und das blaue Viereck zerlegt werden. Auch das Trapez, das Parallelogramm und das Fünfeck können in das rote und das blaue Viereck zerlegt werden. Also ist auch ihr Flächeninhalt acht Kästchen.
-
Flächenvergleich
Flächenmessung
Zum Bestimmen des Flächeninhalts einer Figur kann diese mit Einheitsflächen, zum Beispiel mit Quadraten, ausgelegt werden. Die Maßzahl gibt dann die Anzahl der Einheitsquadrate an, die zum Auslegen der Figur benötigt werden.
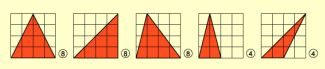
Der Flächeninhalt eines Rechtecks kann als Produkt der Seitenlängen berechnet werden (Bild 3).
Ebenso kann auch der Flächeninhalt von Dreieck, Parallelogramm, Trapez usw. berechnet werden, indem zu diesen Figuren flächengleiche Rechtecke gesucht werden. Grundlage dazu ist u. a. die Satzgruppe des Pythagoras, aber auch der Satz über Ergänzungsparallelogramme, welcher ebenfalls bereits bei EUKLID zu finden ist:
Werden durch einen beliebigen Punkt einer Diagonalen eines Parallelogramms die Parallelen zu den Seiten des Parallelogramms gezeichnet, so sind von den vier entstehenden Teilparallelogrammen die beiden flächengleich, die nicht von der Diagonalen durchschnitten werden.
Der Beweis erfolgt mithilfe der Kongruenz von Dreiecken.
Hieraus ergeben sich eine Reihe von Formeln zur Berechnung der Flächeninhalte einfacher Figuren: Dreiecke, Vierecke, Vielecke.
-
Bestimmen des Flächeninhalts durch Einheitsquadrate
Flächeninhalt unregelmäßiger, krummlinig begrenzter Figuren
Der Flächeninhalt krummlinig begrenzter Figuren kann durch Annäherung (Approximation) beim Auslegen ermittelt werden:
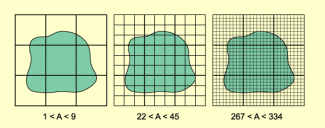
Über die Figur im Bild 4 wird ein quadratisches Raster gelegt. Der Flächeninhalt A der Figur muss dann größer als die Anzahl der vollständig von der Figur eingeschlossenen Quadrate und kleiner als die Anzahl aller von der Figur berührten Quadrate sein. Durch Verkleinerung der Quadrate des Rasters wird die Genauigkeit des Ergebnisses vergrößert.
Auf diese Weise wird der Flächeninhalt mit immer kleineren Einheiten immer genauer angegeben. Der Genauigkeitszuwachs wird noch deutlicher, wenn man alle Angaben in die Einheit „kleines Quadrat“ umrechnet:
81 < A < 729; 198 < A < 405; 267 < A < 334
Flächenmaße
Das grundlegende heutige Flächenmaß ist Quadratmeter. Zeichen:
-
Verkleinerung der Rasterquadrate erhöht die Genauigkeit der Ergebnisse
Es ist definiert als die Fläche eines Quadrates mit der Seitenlänge von 1m. Vom Quadratmeter abgeleitete Einheiten sind:
Besonders in der Landwirtschaft sind noch häufig alte Flächenmaße (historische Maße) im Gebrauch. Am bekanntesten ist der Morgen, welcher in der Regel mit 25 a oder 0,25 ha angeben wird.

