Flächeneinheiten

Die Basiseinheit für Flächen ist der Quadratmeter ( $m^{2}$ ). Für größere oder kleinere Flächen verwendet man Einheiten, die durch Vervielfachen mit Potenzen von $100 = 10^{2}$ aus dem Quadratmeter abgeleitet sind, wie z. B. Quadratkilometer ( $k m^{2}$ ), Hektar (ha), Ar (a), Quadratdezimeter ( $d m^{2}$ ), Quadratzentimeter
( $c m^{2}$ ), Quadratmillimeter ( $m m^{2}$ ).

Die Basiseinheit für Flächen ist der Quadratmeter ( $m^{2}$ ).
Für größere oder kleinere Flächen verwendet man Einheiten, die durch Vervielfachen mit Potenzen von $100 = 10^{2}$ aus dem Quadratmeter abgeleitet sind, wie z. B. Quadratkilometer $(k m^{2})$ , Hektar (ha), Ar (a), Quadratdezimeter $(d m^{2})$ , Quadratzentimeter $(c m^{2})$ , Quadratmillimeter $(m m^{2})$ .

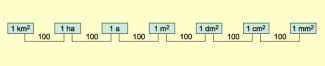
Dabei ergeben sich folgende Umrechnungsfaktoren (Bild 2):
$\begin{array}{l} 1 a = 100 m^{2} \\ 1 h a = 100 a = 100^{2} m^{2} = 10000 m^{2} \\ 1 k m^{2} = 100 h a = 100^{2} a = 100^{3} m^{2} = 1000000 m^{2} \\ 1 d m^{2} = 100^{- 1} m^{2} (100 d m^{2} = 1 m^{2}) \\ 1 c m^{2} = 100^{- 2} m^{2} (10000 c m^{2} = 100 d m^{2} = 1 m^{2}) \\ 1 m m^{2} = 100^{- 3} m^{2} (1000000 m m^{2} = 10000 c m^{2} = 100 d m^{2} = 1 m^{2}) \end{array}$

Es sind einige Beispiele für derartige Umrechnungen angegeben.
Dabei können die gegebenen Ausgangswerte durch eigene ersetzt werden, man erhält dann jeweils den zugehörigen Umrechnungswert.

Übersicht über Umrechnung von Flächeneinheiten

Stand: 2010
Dieser Text befindet sich in redaktioneller Bearbeitung.

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Verwandte Artikel

Flächeneinheiten

Rechtliches

Einloggen