Potenzfunktionen, allgemein
Funktionen mit Gleichungen
der Form
heißen Potenzfunktionen.
Es ist zweckmäßig, eine Einteilung der Potenzfunktionen in Abhängigkeit vom Exponenten n vorzunehmen.
Funktionen mit Gleichungen der Form heißen Potenzfunktionen.
Es ist zweckmäßig, eine Einteilung der Potenzfunktionen in Abhängigkeit vom Exponenten n vorzunehmen:
- Ist der Exponent n in eine gerade Zahl , so liegen gerade Funktionen vor.
Die y-Achse ist die Symmetrieachse für alle diese Funktionsgraphen (Bild 1).
- Ist der Exponent n in eine ungerade Zahl , so liegen ungerade Funktionen vor.
Die Funktionsgraphen sind punktsymmetrisch (zentralsymmetrisch) zum Koordinatenursprung O (Bild 2).
-
Potenzfunktion mit geraden Exponenten
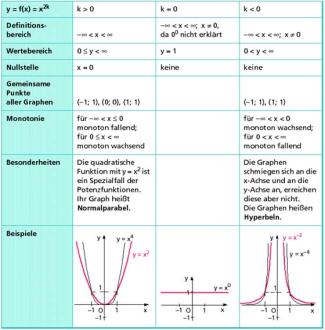
-
Potenzfunktionen mit ungeraden Exponenten
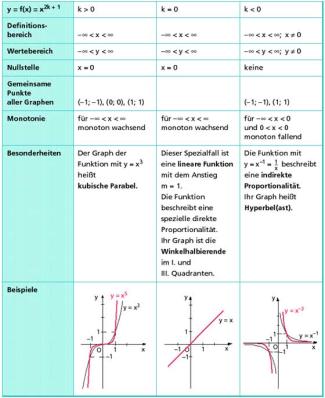
Bezüglich der Potenzfunktionen mit ungeraden Exponenten kann man folgende Fälle unterscheiden.
Die Graphen der Funktion heißen Hyperbeln ersten, dritten … Grades. Sie bestehen aus zwei Teilen, den Hyperbelästen.
Die Funktionen mit sind eineindeutig und lassen sich im gesamten Definitionsbereich umkehren.
Die Umkehrfunktionen heißen Wurzelfunktionen.
Lernhelfer (Duden Learnattack GmbH): "Potenzfunktionen, allgemein." In: Lernhelfer (Duden Learnattack GmbH). URL: http://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/potenzfunktionen-allgemein (Abgerufen: 01. March 2026, 03:23 UTC)

