Pseudozufallszahlen
Die Simulation zufälliger Vorgänge aus der Praxis ist oft sehr mühsam und zeitaufwendig. Das gilt besonders auch für das Erzeugen von Zufallszahlen und das Arbeiten mit diesen Zahlen (ggf. unter Verwendung entsprechender Tabellen).
Heute ist es möglich, von Computern erzeugte Zufallszahlen, sogenannte Pseudozufallszahlen, zu nutzen. Grundlage für deren Erzeugung ist ein Algorithmus, der Ziffernfolgen liefert, die annähernd dieselben Eigenschaften haben wie echte Zufallszahlen.
Die Simulation zufälliger Vorgänge aus Natur, Technik und Gesellschaft durch entsprechende Zufallsexperimente, wie etwa durch Ziehen von Kugeln aus Urnen, ist oft sehr mühsam und zeitaufwendig. Daher liegt es nahe, diese Experimente durch Rechner zu realisieren (zu simulieren). Hierzu werden vom Computer erzeugte Zufallszahlen , sogenannte Pseudozufallszahlen, genutzt, die mithilfe eines (Pseudo-)Zufallsgenerator erzeugt werden.
Grundlage für die Erzeugung ist ein (deterministischer) Algorithmus, der Ziffernfolgen liefert, die annähernd dieselben Eigenschaften haben wie echte Zufallszahlen. Im Allgemeinen benutzen Taschenrechner und Computer die RANDOM-Funktion als Zufallsgenerator , die derartige Algorithmen verwendet und Pseudozufallszahlen zwischen 0 und 1 liefert. Im Folgenden ist ein BASIC-Programm zum Gewinnen solcher Zahlen angegeben:
Auch mithilfe von Tabellenkalkulationsprogrammen kann man sich (Pseudo-)Zufallszahlen ausdrucken lassen.
Zur Überprüfung der „Güte“ der Pseudozufallszahlen gibt es verschiedene Kriterien. Beispielsweise sollte für die relative Häufigkeiten der Ziffern 0 bis 9 gelten:
-
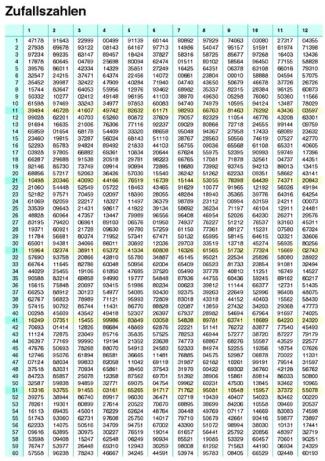
Tabelle mit Zufallsziffern