Quadratische Funktionen, Graphen

Der Graph einer quadratischen Funktion mit der Gleichung y = f   ( x ) = a x 2 + b x + c ist für a = 1 eine (ggf. verschobene) Normalparabel.
Für a ≠ 1 erhalten wir als Graph im Vergleich zum Graphen von y = f   ( x ) = x 2 + b x + c eine (in y-Richtung) gestreckte bzw. gestauchte und gegebenenfalls an der x-Achse gespiegelte Parabel.

Der Graph einer quadratischen Funktion mit der Gleichung y = f   ( x ) = a x 2 + b x + c ist für a = 1 eine (ggf. verschobene) Normalparabel.

Für a ≠ 1 erhalten wir als Graphen im Vergleich zum Graphen von y = f   ( x ) = x 2 + b x + c eine (in y-Richtung) gestreckte bzw. gestauchte und gegebenenfalls an der x-Achse gespiegelte Parabel:
 

a > 1 Parabel ist gestreckt.
0 < a < 1 Parabel ist gestaucht.
−   1 < a < 1 Parabel ist gestaucht und an der x-Achse gespiegelt.
a < −   1 Parabel ist gestreckt und an der x-Achse gespiegelt.


Die Parabel mit der Gleichung y = f   ( x ) = a x 2 besitzt wie die Normalparabel den Scheitelpunkt S   ( 0 ;   0 ) .
Um die Scheitelpunktskoordinaten einer Parabel mit der Gleichung y = f   ( x ) = a x 2 + b x + c mit a ≠ 1 zu ermitteln, formen wir folgendermaßen um:
  a x 2 + b x + c = a   ( x 2 + b a x + c a ) = a   [ ( x 2 + b a x + ( b 2 a ) 2 ) + ( −   ( b 2 a ) 2 + c a ) ] = a   [ ( x + b 2 a ) 2 − b 2 4 a 2 + c a ] = a   ( x + b 2 a ) 2 − b 2 4 a + c = a   ( x 2 + b 2 a ) 2 + 4 a c − b 2 4 a

Der Scheitelpunkt hat also die folgenden Koordinaten:
     S   ( − b 2 a ;   4 a c − b 2 4 a )

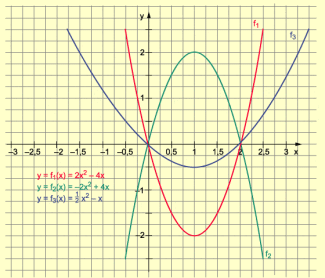
Beispiel 1: Graphen von y = f   ( x ) = a x 2 für verschiedene Werte von a (Bild 1).
 

x– 2–1012
y = f 1   ( x ) = x 2 41014
y = f 2   ( x ) = 2 x 2 82028
y = f 3   ( x ) = 1 2 x 2 2 1 2 0 1 2 2
y = f 4   ( x ) = −     1 2 x 2 – 2 −   1 2 0 −   1 2 – 2
y = f 5   ( x ) = −     2 x 2 – 8– 10– 1– 8
Graphen quadratischer Funktionen durch den Koordinatenursprung

Graphen quadratischer Funktionen durch den Koordinatenursprung

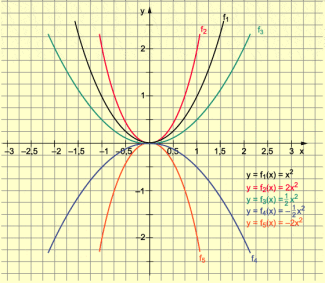
Beispiel 2: Graphen von y = f   ( x ) = a x 2 + b x + c für verschiedene Werte von a (Bild 2).

•     y = f 1   ( x ) = 2 x 2 − 4 x = 2 [ ( x − 1 ) 2 − 1 ] = 2   ( x − 1 ) 2 − 2   ⇒   S ( 1 ;   − 2 )
•     y = f 2   ( x ) = −   2 x 2 + 4 x = −   2 [ ( x − 1 ) 2 − 1 ] = −   2   ( x − 1 ) 2 + 2   ⇒   S ( 1 ;   2 )
•     y = f 3   ( x ) = 1 2 x 2 − x = 1 2 [ ( x − 1 ) 2 − 1 ] = 1 2   ( x − 1 ) 2 − 1 2   ⇒   S ( 1 ;   − 1 2 )

Streckung, Stauchung bzw. Spiegelung von Graphen quadratischer Funktionen

Streckung, Stauchung bzw. Spiegelung von Graphen quadratischer Funktionen

Funktionsgraph Streckung Spiegelung Normalparabel Parabel Rechenbeispiel Stauchung quadratische Funktion Scheitelpunkt Scheitelpunktskoordinaten
Lexikon Share
Mathe Note verbessern?
 

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

  • 40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
  • Hausaufgabenhilfe per WhatsApp
  • Original Klassenarbeiten mit Lösungen
  • Deine eigene Lern-Statistik
  • Kostenfreie Basismitgliedschaft
Mathe kostenlos lernen
Verwandte Artikel
alle anzeigen
Angaben zum Lexikon
Impressum
© Duden Learnattack GmbH, 2024

Einloggen