Verhältnisgleichungen

Viele Probleme, bei denen mit drei gegebenen Größen eine vierte berechnet wird, führen auf Verhältnisgleichungen (Proportionen).
Eine Gleichung der Form
$\frac{\text{a}}{\text{b}}=\frac{\text{c}}{\text{d}}\left(\text{a}\text{,b}\text{,c}\text{,d}\ne \text{0}\right)$
heißt Verhältnisgleichung oder Proportion.
Dabei wird der Quotient zweier Größen als Verhältnis bezeichnet.

Beispiel:
Gegeben sind zwei Würfel mit der Kantenlänge 2 cm bzw. 3 cm (Bild 1).
Das Verhältnis der Kantenlängen beträgt 2 : 3.
Das Verhältnis der Volumina beträgt 8 : 27.

Werden mehr als zwei Verhältnisse betrachtet, so nennt man sie fortlaufende Proportion.

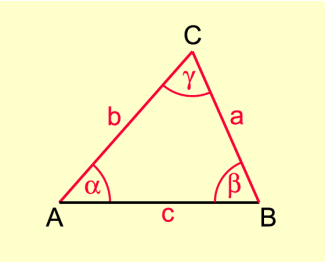
Beispiel (Bild 2):
Sinussatz: $\text{a}\text{:}\text{b}\text{:}\text{c}=\text{sin}\alpha \text{:}\text{sin}\beta \text{:}\text{sin}\gamma \text{bzw}\text{.}\frac{\text{a}}{\text{sin}\alpha }=\frac{\text{b}}{\text{sin}\beta }=\frac{\text{c}}{\text{sin}\gamma }$
Verhältnisgleichungen haben auch eine große Bedeutung bei der Prozentrechnung, bei den Strahlensätzen und bei linearen Funktionen der Form y = mx.

Verhältnisgleichungen lassen sich mithilfe der Regeln für das äquivalente Umformen von Gleichungen lösen.

Beispiel:
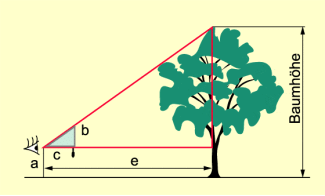
Mithilfe eines sogenannten Försterdreiecks lässt sich die Höhe eines Baums bestimmen (Bild 3).
 

Lösung:
$\begin{array}{l}\frac{x–a}{e}=\frac{\text{b}}{\text{c}}|\cdot \text{e}\\ \text{x}-\text{a}=\frac{\text{b}\cdot \text{e}}{\text{c}}|+\text{a}\\ \text{x}=\frac{\text{b}\cdot \text{e}}{\text{c}}+\text{a}\\ \text{x}=\frac{\text{0}\text{,20}\text{m}\cdot \text{25}\text{m}}{\text{0}\text{,30}\text{m}}+\text{1}\text{,70}\text{m}\\ \text{x }\approx \text{18}\text{m }\end{array}$

Anwort: Der Baum hat eine Höhe von etwa 18 m.

Eine Verhältnisgleichung lässt sich in den folgenden Formen schreiben:
$\begin{array}{l}\text{a}\text{:}\text{b}=\text{c}\text{:}\text{d}\\ \frac{\text{a}}{\text{b}}=\frac{\text{c}}{\text{d}}\\ \text{a}\cdot \text{d}=\text{b}\cdot \text{c}\end{array}$
Die letzte Gleichung wird Produktgleichung genannt.

In jeder Verhältnisgleichung ist das Produkt der Innenglieder gleich dem Produkt der Außenglieder:
$a\cdot d=b\cdot c$

Es lassen sich beide Innenglieder, beide Außenglieder, Innen- gegen Außenglieder und beide Seiten einer Verhältnisgleichung vertauschen (Bild 4).
Aus der Verhältnisgleichung $\frac{\text{a}}{\text{b}}=\frac{\text{c}}{\text{d}}\left(\text{a}\text{,b}\text{,c}\text{,d}\ne \text{0}\right)$ erhält man durch korrespondierende Addition bzw. Subtraktion die folgenden gleichwertigen Verhältnisgleichungen:
$\begin{array}{l}\frac{\text{a}+\text{b}}{\text{b}}=\frac{\text{c}+\text{d}}{\text{d}}\frac{\text{a}-\text{b}}{\text{b}}=\frac{\text{c}-\text{d}}{\text{d}}\\ \frac{\text{a}}{\text{b}+\text{a}}=\frac{\text{c}}{\text{d}+\text{c}}\frac{\text{a}}{\text{b}-\text{a}}=\frac{\text{c}}{\text{d}-\text{c}}\end{array}$

Beispiel:
$\text{Aus}\frac{\text{x}-\text{a}}{\text{b}-\text{x}}=\frac{\text{a}}{\text{x}}\text{ ergibt}\text{sich}\text{b}\text{:}\text{x}=\text{x}\text{:}\text{a}\text{.}$
Löst man die Gleichung nach x auf, so erhält man:
$\text{x}=\sqrt{\text{a}\cdot \text{b}}$
Diese Wurzel aus dem Produkt zweier Zahlen a und b wird auch als deren geometrisches Mittel bezeichnet.