Mechanische Arbeit
Mechanische Arbeit wird verrichtet, wenn ein Körper bzw. ein System durch eine Kraft bewegt oder verformt wird.
| Formelzeichen: | W |
| Einheiten: | ein Newtonmeter ( 1 Nm) ein Joule (1 J) |
Die mechanische Arbeit beschreibt einen Prozess; sie ist daher im Unterschied zur Energie eine Prozessgröße. In Abhängigkeit von den gegebenen Bedingungen können die verschiedenen Arbeiten mechanischer Arbeit (Hubarbeit, Beschleunigungsarbeit, Reibungsarbeit, Verformungsarbeit) berechnet oder aus einem Kraft-Weg-Diagramm ermittelt werden.
Arbeit im Alltag und in der Physik
Im Alltag bezeichnet man Tätigkeiten, bei denen wir uns anstrengen und verausgaben müssen, als Arbeit. Solche Tätigkeiten sind z. B. das Tragen eines Koffers, das Fahren mit dem Fahrrad, das Dehnen eines Expanders oder das Lernen von Vokabeln. Man spricht von geistiger Arbeit oder von der Klassenarbeit. Im Unterschied zu diesem vielfältigen Gebrauch des Begriffs „Arbeit“ in der Umgangssprache ist der Begriff in der Physik eindeutig definiert: Mechanische Arbeit ist immer verbunden mit der Bewegung oder Verformung von Körpern oder Systemen durch Einwirken einer Kraft.
Definition des Begriffs mechanische Arbeit
Mechanische Arbeit wird verrichtet, wenn ein Körper bzw. ein System durch eine Kraft bewegt oder verformt wird.
Eine Arbeit von 1 Nm wird verrichtet, wenn an einem Körper eine Kraft von 1 N angreift und der Körper dadurch 1 m in Richtung der wirkenden Kraft bewegt wird. Die Einheit ein Newtonmeter wird zu Ehren des englischen Physikers JAMES PRESCOTT JOULE (1818-1889) auch als ein Joule (sprich: ein dschul) bezeichnet. Es gilt:
1 Nm = 1 J
In der nachfolgenden Übersicht sind einige Beträge von Arbeiten für einige spezielle Fälle angegeben.![]()
-

L. Meyer, Potsdam
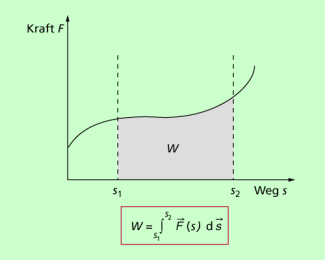
Die mechanische Arbeit kann allgemein mithilfe folgender Gleichung berechnet werden:
Es ist das Skalarprodukt aus Kraft und Weg. Im Kraft-Weg-Diagramm (Bild 2) ist die Arbeit gleich der Fläche unter dem Graphen. Man kann damit die mechanische Arbeit auch durch Auszählen der betreffenden Fläche ermitteln, wenn das F-s-Diagramm bekannt ist.
Der Begriff Arbeit als Produkt aus Kraft und Weg wurde von dem französischen Mathematiker J. V. PONCELET (1788-1867) mit Unterstützung des französischen Ingenieurs und Physikers G. G. CORIOLIS (1792-1843) um 1826 in die Physik eingeführt.
Spezielle Fälle der mechanischen Arbeit
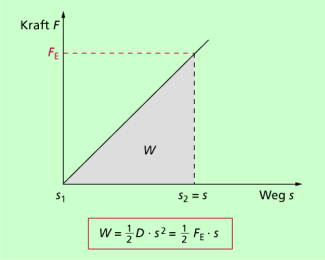
Vergrößert sich die Kraft gleichmäßig mit dem Weg, wie das z.B. bei Dehnen einer Feder im elastischen Bereich der Fall ist (Bild 3), dann kann man diese Federspannarbeit folgendermaßen berechnen:
Für die Kraft bei einer Feder gilt:
Dabei ist D die Federkonstante und s die Dehnung der Feder. Setzt man diese Kraft in die allgemeine Definitionsgleichung ein und geht man von der gleichen Richtung von Kraft und Weg aus, dann erhält man:
Das ist die üblicherweise angegebene Gleichung für die Federspannarbeit. Aus Bild 3 ist erkennbar, dass man die genannte Gleichung auch sehr einfach aus dem F-s-Diagramm ableiten kann. Geht man davon aus, dass die Fläche unter dem Graphen gleich der verrichteten mechanischen Arbeit ist, dann ergibt sich:
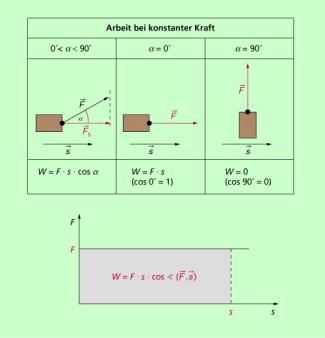
Ist die wirkende Kraft konstant, dann erhält man für die mechanische Arbeit die allgemeine Gleichung:
Für dieses skalare Produkt kann man auch schreiben:
Daraus ergeben sich die in Bild 4 dargestellten Fälle. Im F-s-Diagramm (Bild 4) ist auch hier die Arbeit die Fläche unter dem Graphen.
Arten mechanischer Arbeit
Je nach der Art und Weise, wie mechanische Arbeit verrichtet wird, unterscheidet man verschiedene spezielle Arten mechanischer Arbeit .
Wird ein Körper durch eine Kraft gehoben, so wird Hubarbeit (Bild1) verrichtet. Dabei wirkt in der Regel eine konstante Kraft in Richtung der Bewegung. Wird die Bewegung eines Körpers durch eine Reibungskraft gehemmt, so spricht man von Reibungsarbeit . Wird ein Körper durch eine Kraft beschleunigt, so wird an ihm Beschleunigungsarbeit verrichtet. Wird ein Körper durch eine Kraft verformt, so spricht man von Verformungsarbeit , im Falle der Verformung einer Feder von Federspannarbeit . Wird durch eine Kraft das Volumen eines eingeschlossenen Gases verringert, so wird an dem Gas Volumenänderungsarbeit oder Volumenarbeit verrichtet.
Genauere Informationen zu den einzelnen Arten der mechanischen Arbeit sind unter den betreffenden Stichwörtern gegeben.
Zusammenhang zwischen Arbeit und Energie
Wird an einem Körper bzw. System oder von einem Körper bzw. System mechanische Arbeit verrichtet, so verändert sich dessen Energie . So vergrößert sich z. B. beim Heben eines Körpers dessen potenzielle Energie. Beim Beschleunigen eines Autos vergrößert sich dessen kinetische Energie, beim Abbremsen wird sie kleiner. Beim Verrichten von Reibungsarbeit verringert sich dessen kinetische Energie. Allgemein gilt:
Die von einem Körper bzw. System oder an einem Körper bzw. System verrichtete mechanische Arbeit ist gleich der Änderung seiner Energie.
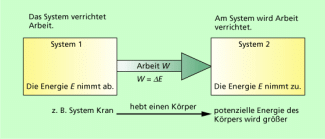
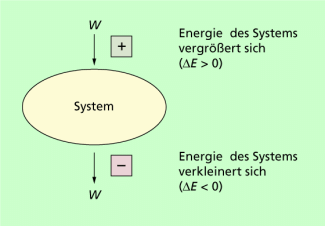
Diese Zusammenhänge sind in Bild 5 dargestellt. Es gilt allgemein:
Für das Vorzeichen der Arbeit ergibt sich aus diesen Betrachtungen als allgemein übliche Festlegung in der Physik (Bild 6):
| |
|
Suche nach passenden Schlagwörtern
- Volumenänderungsarbeit
- Berechnung
- Prozessgröße
- Skalarprodukt
- Newtonmeter
- Hubarbeit
- Volumenarbeit
- F-s-Diagramm
- Federspannarbeit
- Joule
- Arten mechanischer Arbeit
- skalares Produkt
- Energie
- Vorzeichen der Arbeit
- Verformungsarbeit
- Rechenbeispiel
- Mechanische Arbeit
- Reibungsarbeit
- Beschleunigungsarbeit
- Kraft-Weg-Diagramm