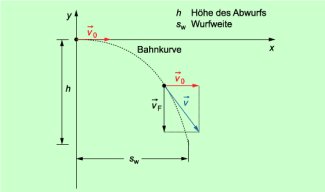
Waagerechter Wurf

Für die Überlagerung von Bewegungen gilt das Unabhängigkeitsprinzip, das auch als Superpositionsprinzip bezeichnet wird. Es lautet:

Führt ein Körper gleichzeitig mehrere Teilbewegungen aus, so überlagern sich diese Teilbewegungen unabhängig voneinander zu einer resultierenden Gesamtbewegung.

Für die Geschwindigkeiten in x-Richtung und in y-Richtung gilt:

$\begin{array}{l}{v}_{\text{x}}=v_0\text{(konstante Abwurfgeschwindigkeit)}\\ v_{\text{y}}=-g\cdot t\text{(freier Fall)}\end{array}$

Die Geschwindigkeiten addieren sich vektoriell (Bild 1). Da sie senkrecht zueinander verlaufen, gilt für die resultierende Geschwindigkeit:

$v=\sqrt{v_0^2+{(g\cdot t)}^2}$

Sie kann auch zeichnerisch ermittelt werden. In analoger Weise ergeben sich für die Wege in x-Richtung und in y-Richtung:

$\begin{array}{l}{s}_{\text{x}}=x=v_0\cdot t\text{(1)}\\ s_{\text{y}}=y=-\frac{g}{2}{t}^2\text{(2)}\end{array}$

Die Gleichung für die Bahnkurve ergibt sich aus den beiden zuletzt genannten Gleichungen. Dazu wird Gleichung (1) nach t umgestellt und in Gleichung (2) eingesetzt:

$\begin{array}{l}\text{Aus}x=v_0\cdot t\text{erhält man}t=\frac{x}{v_0}.\\ \text{Eingesetzt in}y=-\frac{g}{2}{t}^2\text{ergibt:}\\ y=-\frac{g}{2}\cdot \frac{x^2}{v_0^2}\text{oder in der üblichen Schreibweise:}\\ y=-\frac{g}{2\cdot v_0^2}{x}^2\end{array}$

Das ist die Gleichung für eine Parabel. Sie wird in der Physik als Wurfparabel bezeichnet.
Wird ein Körper aus einer Höhe h abgeworfen, wie das z.B. bei einem waagerecht abgeworfenen Ball der Fall ist, so beträgt die Wurfweite:

$s_W=\sqrt{\frac{2v_0^2\cdot h}{g}}$

Diese Gleichung ergibt sich, wenn man als Abwurfpunkt den Ursprung des Koordinatensystems wählt. Dann ist die Bezugshöhe, auf der man die Wurfweite misst, gleich -h. Setzt man in die oben genannte Gleichung für die Wurfparabel y = -h und stellt die Gleichung nach x um, so erhält man die Gleichung für die Wurfweite. Sie ist also gleich dem x-Wert für y = -h.