Ganzrationale Funktionen

Eine Funktion $f$ , deren Funktionsterm ein Polynom ist, heißt ganzrationale Funktion (bzw. Polynomfunktion).
Ganzrationale Funktionen haben die folgende Form:
$\begin{array}{l} f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{2} x^{2} + a_{1} x + a_{0} \\ (mit n \in ℕ und a_{i} \in ℝ) \end{array}$
Ist $a_{n} \neq 0$ , so hat $f$ den Grad $n$ .

Ganzrationale Funktionen

#Ganzrationale Funktionen #Analysis #Spezielle Funtionen #Polynome #Graphen #Grad #Koeffizient #Eigenschaften von Funktionen #Symmetrie #Wertebereich #Definitionsbereich #Monotonie #Asymptote #Funktionsgraph

Übungen und Erklärvideos zu ganzrationalen Funktionen gibt es auf learnattack.de

Der Deutsche Wetterdienst (DWD) betreibt bundesweit etwa 480 Klimastationen. Die Betreuer dieser nebenamtlichen Wetterstationen haben vielfältige Aufgaben. Registriert werden z.B. Windstärke, Windrichtung, relative Luftfeuchtigkeit, Sichtweite, Bewölkung u.a.m. Mehrmals täglich wird die Temperatur gemessen. Ein sogenannter Thermograf zeichnet die Temperaturkurve auf. Jeder Uhrzeit wird dabei eine ganz bestimmte Temperatur zugeordnet. Solche Zuordnungen zwischen zwei Größen, die den funktionalen Zusammenhang zwischen diesen beschreiben, werden als Funktionen bezeichnet.

In der Mathematik versteht man unter einer Funktion $f$ eine eindeutige Zuordnung. Dabei wird jedem $x \in D_{f}$ genau ein $y \in W_{f}$ zugeordnet. Dabei ist $D_{f}$ der Definitionsbereich (die Definitionsmenge) und $W_{f}$ der Wertebereich (die Wertemenge) der Funktion $f$ .

In der Analysis beschäftigt man sich ausschließlich mit Funktionen, bei denen Definitions- und Wertebereich Mengen reeller Zahlen sind. In diesem Zusammenhang spricht man von reellen Funktionen.

Die reellen Funktionen lassen sich in bestimmte Funktionsarten einteilen. Je nachdem, ob bei der Verknüpfung der Funktionsvariablen nur rationale Rechenoperationen (also die bekannten Grundrechenoperationen) oder darüber hinaus noch weitere Rechenoperationen vorkommen, unterscheidet man rationale Funktionen und nichtrationale Funktionen. Die rationalen Funktionen werden nochmals in ganzrationale und gebrochenrationale Funktionen unterteilt.

Bild

Zur Erklärung des Begriffs ganzrationale Funktion benötigt man den Polynombegriff. Polynome entstehen, wenn Terme der Form $a_{i} x^{n}$ mit $a_{i} \neq 0$ und $n \in ℕ$ addiert oder subtrahiert werden. Polynome werden in der Regel nach der höchsten Potenz von $x$ , dem Grad des Polynoms, geordnet und benannt. Die $a_{i}$ heißen Koeffizienten des Polynoms und sind stets reelle Zahlen.

Eine Funktion $f$ , deren Funktionsterm ein Polynom ist, heißt ganzrationale Funktion (bzw. Polynomfunktion).
Ganzrationale Funktionen haben die folgende Form:
$f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{2} x^{2} + a_{1} x + a_{0} ($ mit $n \in ℕ$ und $a_{i} \in ℝ)$
Ist $a_{n} \neq 0$ , so hat $f$ den Grad $n$ .

Wir betrachten im Folgenden einige Beispiele ganzrationaler Funktionen:

Die Funktion $f$ mit $f (x) = 8$ ist eine konstante Funktion.
Konstante Funktionen haben die Form $f (x) = a_{i} = c$ , ihr Grad ist 0.
Die Funktion $f$ mit $f (x) = 3 x - 5$ ist eine lineare Funktion.
Lineare Funktionen (bzw. Funktionen 1. Grades) haben die Form $f (x) = a_{1} x + a_{0}$ .
Die Funktion $f$ mit $f (x) = 3 x^{2} + 5 x - 12$ ist eine quadratische Funktion.
Quadratische Funktionen (bzw. Funktionen 2. Grades) haben die Form $f (x) = a_{2} x^{2} + a_{1} x + a_{0}$ .
Die Funktion $f$ mit $f (x) = - 5 x^{3} + 2,5 x^{2} + 0,2 x - 4$ ist eine kubische Funktion.
Kubische Funktionen (Funktionen 3. Grades) haben die Form $f (x) = a_{3} x^{3} + a_{2} x^{2} + a_{1} x + a_{0}$ .
Die Funktion $f$ mit $f (x) = 9 x^{4} - \sqrt{2} x + 4$ ist eine ganzrationale Funktion 4. Grades mit $a_{4} = 9, a_{3} = a_{2} = 0, a_{1} = - \sqrt{2}$ und $a_{0} = 4$ .
Die Funktion $f$ mit $f (x) = x \cdot (x + 5) - x^{2} + 4$ ist wegen $f (x) = x \cdot (x + 5) - x^{2} + 4 = x^{2} + 5 x - x^{2} + 4 = 5 x + 4$ eine lineare Funktion.

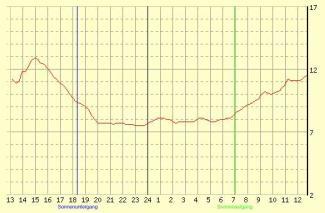
Aufgezeichneter Temperaturverlauf für 24 Stunden an einem Ort Deutschlands im Januar 2003

Anmerkung: Die Funktion $f$ mit $f (x) = \frac{x^{3}}{x - 1}$ ist keine ganzrationale Funktion, da man den Funktionsterm nicht auf die Form $a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{1} x + a_{0}$ bringen kann.

Verhalten ganzrationaler Funktionen für betragsmäßig große Werte von x

Es soll untersucht werden, wie sich ganzrationale Funktionen für betragsmäßig große (d.h. sehr kleine bzw. sehr große) $x$ verhalten.

Als Beispiel für dieses zu untersuchende Verhalten im Unendlichen betrachten wir die kubische Funktion $f$ mit $f (x) = 3 x^{3} - 4 x^{2} + 1$ . Für diese ergeben sich beispielsweise die folgenden Funktionswerte:

$\begin{matrix} \begin{array}{l} f (10) = 2 601 \\ f (100) \approx 2,960 \cdot 10^{6} \\ f (1 000) \approx 2,996 \cdot 10^{9} \\ f (10 000) \approx 3,000 \cdot 10^{12} \end{array} & \begin{array}{l} f (- 10) = - 3 999 \\ f (- 100) \approx - 3,040 \cdot 10^{6} \\ f (- 1 000) \approx - 3,004 \cdot 10^{9} \\ f (- 10 000) \approx - 3,000 \cdot 10^{12} \end{array} \end{matrix}$

Das führt zur Vermutung, dass die Funktionswerte von $f$ für sehr große und sehr kleine $x$ -Werte mit denen von $f (x) = 3 x^{3}$ übereinstimmen.

Das lässt sich relativ einfach bestätigen. Durch Umformen des Funktionsterms (Ausklammern der größten Potenz von $x$ ) erhält man die folgende Darstellung:
$f (x) = x^{3} \cdot (3 - \frac{4}{x} + \frac{1}{x^{3}})$

Die beiden Summanden $- \frac{4}{x}$ und $\frac{1}{x^{3}}$ nähern sich für betragsmäßig große $x$ immer mehr dem Wert Null. Damit gilt in der Tat $f (x) \approx 3 x^{3}$ .

Unsere Überlegungen lassen sich auf alle ganzrationalen Funktionen übertragen, denn es ist:
$\begin{array}{l} f (x) = a_{n} x^{n} + a_{n - 1} x^{n - 1} + ... + a_{2} x^{2} + a_{1} x + a_{0} \\ = x^{n} \cdot (a_{n} + \frac{a_{n - 1}}{x} + ... + \frac{a_{2}}{x^{n - 2}} + \frac{a_{1}}{x^{n - 1}} + \frac{a_{0}}{x^{n}}) \end{array}$

Für betragsmäßig große Werte für $x$ unterscheidet sich die Summe in der Klammer nur sehr wenig von $a_{n}$ an, so dass $f (x) \approx a_{n} x^{n}$ ist.

Das Verhalten einer ganzrationalen Funktion vom Grade $n$ wird für betragsmäßig große Werte für $x$ vom Produkt $a_{n} \cdot x^{n}$ bestimmt.

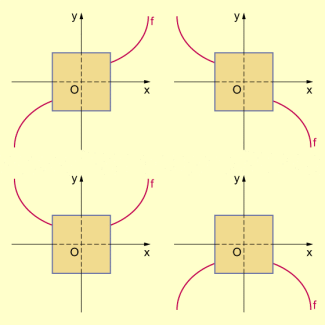
Die Abbildung zeigt das mögliche Verhalten ganzrationaler Funktionen für $x \to \pm \infty$ .

Verlauf ganzrationaler Funktionen für betragsmäßig große x

Mathe Note verbessern?

Kostenlos bei Duden Learnattack registrieren und ALLES 48 Stunden testen.

Kein Vertrag. Keine Kosten.

40.000 Lern-Inhalte in Mathe, Deutsch und 7 weiteren Fächern
Hausaufgabenhilfe per WhatsApp
Original Klassenarbeiten mit Lösungen
Deine eigene Lern-Statistik
Kostenfreie Basismitgliedschaft

Mathe kostenlos lernen

Ganzrationale Funktionen

Ganzrationale Funktionen

Verhalten ganzrationaler Funktionen für betragsmäßig große Werte von x

Rechtliches

Einloggen